Policy Certificates and Minimax-Optimal PAC Bounds for Episodic Reinforcement Learning

August 28, 2019

Figure 1: Comparison of existing algorithms without policy certificates (top) and with our proposed policy certificates (bottom). While in existing reinforcement learning the user has no information about how well the algorithm will perform in the next episode, we propose that algorithms output policy certificates before playing an episode to allow users to intervene if necessary.

Designing reinforcement learning methods which find a good policy with as few samples as possible is a key goal of both empirical and theoretical research. On the theoretical side there are two main ways, regret- or PAC (probably approximately correct) bounds, to measure and guarantee sample-efficiency of a method. Ideally, we would like to have algorithms that have good performance according to both criteria, as they measure different aspects of sample efficiency and we have shown previously [1] that one cannot simply go from one to the other. In a specific setting called tabular episodic MDPs, a recent algorithm achieved close to optimal regret bounds [2] but there was no methods known to be close to optimal according to the PAC criterion despite a long line of research. In our work presented at ICML 2019, we close this gap with a new method that achieves minimax-optimal PAC (and regret) bounds which match the statistical worst-case lower bounds in the dominating terms.

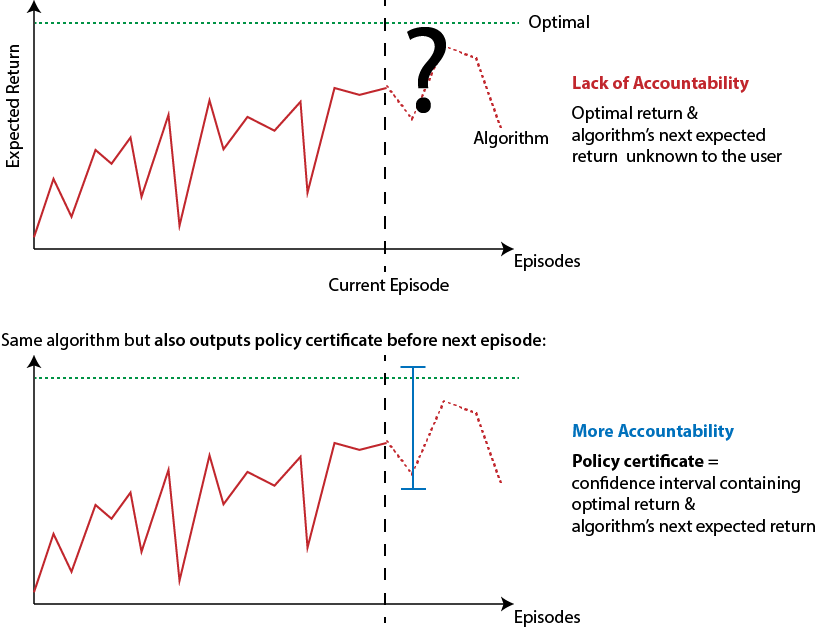
Interestingly, we achieve this by addressing a general issue of PAC and regret bounds which is that they do not reveal when an algorithm will potentially take bad actions (only e.g. how often). This issue leads to a lack of accountability that could be particularly problematic in high-stakes applications (see a motivational scenario in Figure 2).

Besides being sample-efficient, our algorithm also does not suffer from this lack of accountability because it outputs what we call policy certificates. Policy certificates are confidence intervals around the current expected return of the algorithm and optimal return given to us by the algorithm before each episode (see Figure 1). This information allows users of our algorithms to intervene if the certified performance is not deemed adequate. We accompany this algorithm with a new type of learning guarantee called IPOC that is stronger than PAC, regret and the recent Uniform-PAC [1] as it ensures not only sample-efficiency but also the tightness of policy certificates. We primarily consider the simple tabular episodic setting where there is only a small number of possible states and actions. While this is often not the case in practical applications, we believe that the insights developed in this work can potentially be used to design more sample-efficient and accountable reinforcement learning methods for challenging real-world problems with rich observations like images or text.

Figure 2: Existing learning guarantees in reinforcement learning like PAC and regret bounds guarantee the performance of an algorithm over many episodes. They do not tell us when — in which episodes — an algorithm performs badly and only allow us to make statements like the one on the left. In contrast, policy certificates certify the performance for an individual episode in combination with our new IPOC guarantees, we can make statements on the right. (Image adapted from Doctor with Patient Cartoon.svg from Wikimedia Commons by Videoplasty.com, CC-BY-SA 4.0)

We propose to make methods for episodic reinforcement learning more accountable by having them output a policy certificate before each episode. A policy certificate is a confidence interval [l, u]. This interval contains both the expected sum of rewards of the algorithm’s policy in the next episode and the optimal expected sum of rewards in the next episode (see Figure 1 for an illustration). As such, a policy certificate helps answer two questions which are of interest in many applications:

What return is the algorithm’s policy expected to achieve in the next episode? — At least the lower end of the interval l.
How far from optimal is the algorithm’s policy in the next episode? — At most the length of the interval u-l

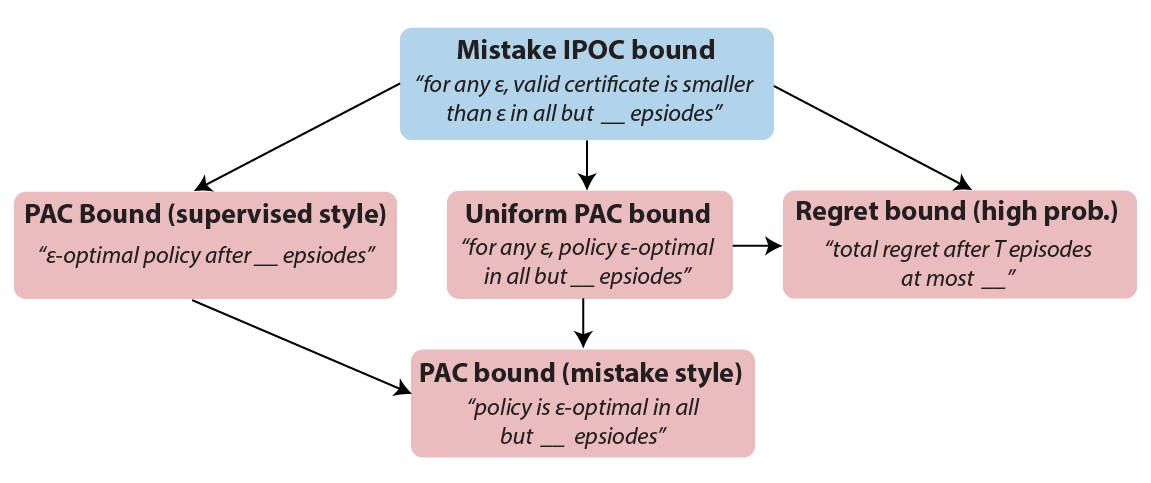
Policy certificates are only useful if these confidence intervals are not too loose. To ensure this, we introduce a type of guarantee for algorithms with policy certificates IPOC (Individual POlicy Certificates) bounds. These bounds guarantee that all certificates are valid confidence intervals and bound the number of times their length can exceed any given threshold. IPOC bounds guarantee both the sample-efficiency of policy learning and the accuracy of policy certificates. That means the algorithm has to play better and better policies but also needs to tell us more accurately how good these policies are. IPOC bounds are stronger than existing learning bounds such as PAC or regret (see Figure 3) and imply that the algorithm is anytime interruptible (see paper for details).

Figure 3: Our (Mistake) IPOC bounds imply bounds in existing frameworks for finite-sample learning guarantees that are similarly tight (see paper for details).

Policy certificates are not limited to specific types of algorithms but optimistic algorithms are particularly natural to extend to output policy certificates. These methods give us the upper end of certificates “for free” as they maintain an upper confidence bound U(s,a) on the optimal value function Q*(s,a) and follow the greedy policy π with respect to this upper confidence bound. In similar fashion, we can compute a lower confidence bound L(s,a) of the Q-function Q(s,a) of this greedy policy. The certificate for this policy is then just these confidence bounds evaluated at the initial state s₁ of the episode [l, u] = [L(s₁, π(s₁)), U(s₁, π(s₁)]

We demonstrate this principle with a new algorithm called ORLC (Optimistic RL with Certificates) for tabular MDPs. Similar to existing optimistic algorithms like UCBVI [2] and UBEV [1], it computes the confidence bounds U(s,a) by optimistic value iteration on an estimated model but also computes lower confidence bounds L(s,a) with a pessimistic version of value iteration. These procedures are similar to vanilla value iteration but add optimism bonuses or subtract pessimism bonuses in each time step respectively to ensure high confidence bounds.

Interestingly, we found that computing lower confidence bounds for policy certificates can also improve sample-efficiency of policy learning. More concretely, we could tighten the optimism bonuses in our tabular method ORLC using the lower bounds L(s,a). This makes the algorithm less conservative and able to adjust more quickly to observed data. As a result, we were able to prove the first PAC bounds for tabular MDPs that are minimax-optimal in the dominating term:

Theorem: Minimax IPOC Mistake, PAC and regret bound of ORLC

In any episodic MDP with S states, A actions and an episode length H, the algorithm ORLC satisfies the IPOC Mistake bound below. That is, with probability at least 1-δ, all certificates are valid confidence intervals and for all ε > 0 ORLC outputs certificates larger than ε in at most

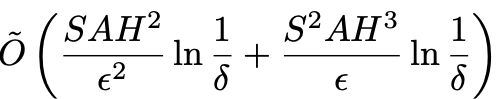
episodes. This immediately implies that the bound above is a (Uniform-)PAC bound and that ORLC satisfies a high-probability regret bound for all number of episodes T of

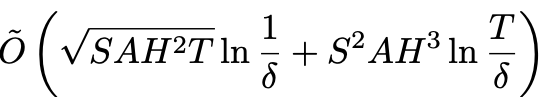
Comparing the order of our PAC bounds against the statistical lower bounds and prior state of the art PAC and regret bounds in the table below, this is the first time the optimal polynomial dependency of SAH² has been achieved in the dominating 1/ε² term. Our bounds also improve the prior regret bounds of UCBVI by avoiding their √(H³T) terms, making our bounds minimax-optimal even when the episode length H is large.

Comparison of prior PAC and regret bounds for this setting. Constants and log-terms are omitted for readability.

As mentioned above, our algorithm achieves this new IPOC guarantee and improved PAC bounds by maintaining a lower confidence bound L(s,a) of the Q-function Q(s,a) of its current policy at all times in addition to the usual upper confidence bound U(s,a) on the optimal value function Q(s,a). Deriving tight lower confidence bounds _L_(s,a) requires new techniques compared to those for upper confidence bounds . All recent optimistic algorithms for tabular MDPs leverage for their upper confidence bounds that _U_ is a confidence bound on _Q_ which does not depend on the samples. The optimal Q-function is always the same, no matter what samples the algorithm saw. We cannot leverage the same insight for our lower confidence bounds because the Q-function of the current policy Q does depend on the samples the algorithm saw. After all, the policy π is computed as a function of these samples. We develop a technique that allows us to deal with this challenge by explicitly incorporating both upper and lower confidence bounds in our bonus terms. It turns out that this technique not only helps achieving tighter lower confidence bounds but also tighter upper-confidence bounds. This is the key for our improved PAC and regret bounds.

Our work provided the final ingredient for PAC bounds for episodic tabular MDPs that are minimax-optimal up to lower-order terms and also established the foundation for policy certificates. In the full paper, we also considered more general MDPs and designed a policy certificate algorithm for so-called finite MDPs with linear side information. This is a generalization of the popular linear contextual bandit setting and requires function approximation. In the future, we plan to investigate policy certificates as a useful empirical tool for deep reinforcement learning techniques and examine whether the specific form of optimism bonuses derived in this work can inspire more sample-efficient exploration bonuses in deep RL methods.

This post is also featured on the ML@CMU blog and is based on the work in the following paper:

Christoph Dann, Lihong Li, Wei Wei, Emma Brunskill Policy Certificates: Towards Accountable Reinforcement Learning International Conference on Machine Learning (ICML) 2019