We often use machine learning to try to uncover patterns in data. In order for those patterns to be useful they should be meaningful and express some underlying structure. Geometry deals with such structure, and in machine learning we especially leverage local geometry. This can be seen in the Euclidean-inspired loss functions we use for generative models as well as for regularization. However, global geometry, which is the focus of Topology, also deals with meaningful structure, the only difference being that the structure is global instead of local. Topology is at present less exploited in machine learning, which is also why it is important to make it more available to the machine learning community at large.
Still, topology applied to real world data using persistent homology has started to find applications within machine learning (including deep learning), but again, compared to its sibling local geometry, it is heavily underrepresented in these domains. In this post, we provide a high-level description of how our TopologyLayer allows (in just a few lines of PyTorch) for backpropagation through Persistent Homology computations and provides instructive, novel, and useful applications within machine learning and deep learning.
As a teaser, consider Figure 1 below. We will show how, in just a few lines of code and a few iterations of SGD, we can define a topology loss and make a generator go from outputting images such as those on the left hand side to those on the right hand side, improving the topological fidelity.

The Gist
Many of us have seen the continuous deformation of a mug into a donut used to explain topology, and indeed, topology is the study of geometric properties that are preserved under continuous deformation. Such properties include number of connected components, number of rings or holes, and the number of voids.

However, in many real world situations, data doesn’t come with an immediate sense of connectivity and neighborhood, and seeing every data point as merely its own connected component is not very interesting. Persistent homology was introduced to study topological properties under a continuously growing range (\(\epsilon \geq 0\)) of estimates of neighborhoods around the points, such that points are considered connected if their neighborhoods intersect. Under this growing estimate the topology of the space changes, and persistent homology provides us with a Persistence Diagram that shows when topological features appear (birth time) and disappear (death time). This gives us an informative overview of the topology of the data under different perspectives, and the ability to naturally consider those topological features that are present under a greater range (with a greater lifetime) of our estimate of neighborhood as more significant.
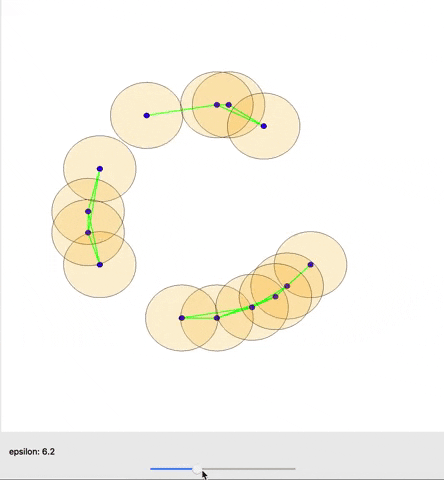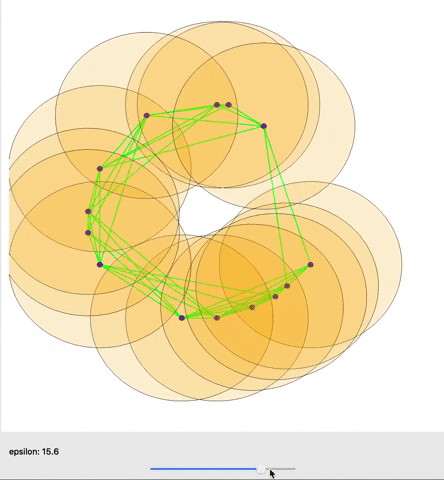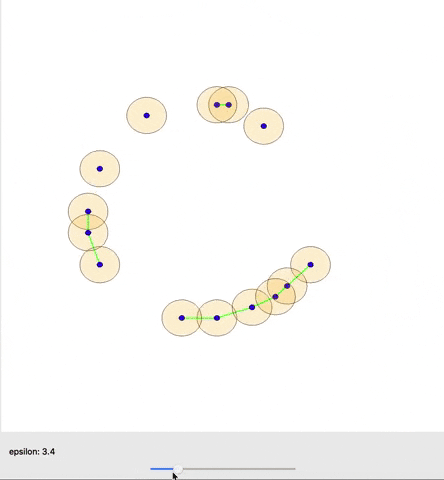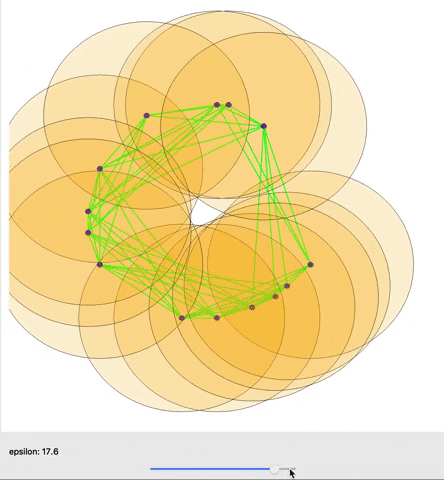
In many situations, it is possible to establish an invertible map from the birth and death time of a topological feature to a pair of points in the data. This map allows us to backpropagate from a loss function on the persistence diagram (the list of topological features with their birth and death times) to the underlying data. In doing so, we can use gradient descent to change the data to minimize our loss and encourage a wide array of topological structures expressed via our loss function. This includes a diverse set of structures, with some showcased in Figure 4 below, where we start with a random collection of points (top center) and use SGD to encourage specific topological features.
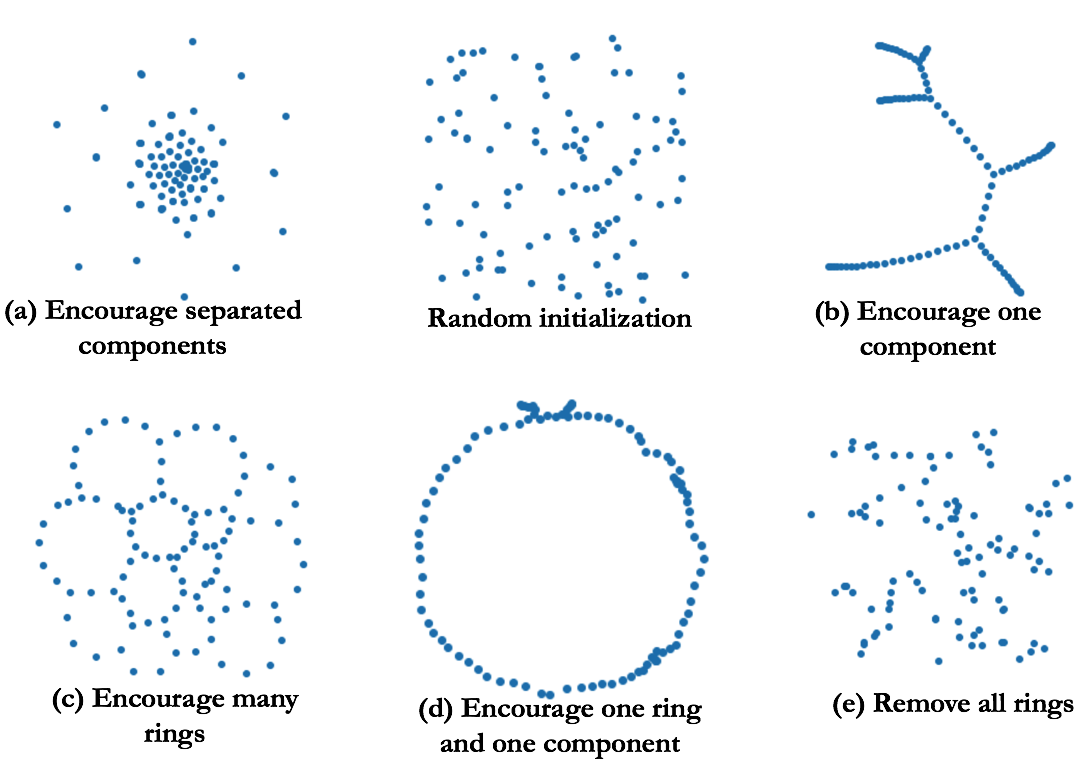
Some Details…
As mentioned, above we described distance-based filtrations (ie filtering operations over connections based on distance), but other filtrations that are also very useful include level set filtrations. Instead of thinking about neighborhoods as growing balls around each point, level set filtrations consider all components that are below (for sublevel filtrations) a growing threshold as ‘connected’. If Figure 5 makes sense to you and you don’t yearn for a more precise deposition, you may skip ahead to the next section and look at the results.
Sounds iffy? Ok, let me provide a little mathematical rigor. In fact, persistent homology is a very general framework that can compute topological features from many different perspectives and on many different spaces – which may be very different from what might appear most natural to us on data in an euclidean space. If you’re interested in getting the complete picture check out this book.
We will consider geometric simplicial complexes, where the vertices correspond to points in some ambient space, e.g. \(\mathbb{R}^d\), although the simplices need not be embedded in the space. Persistent homology studies an increasing sequence of simplicial complexes, or a filtration, \(\emptyset = \mathcal{X}_0 \subset \mathcal{X}_1 \subset ... \subset \mathcal{X}_0 = \mathcal{X}\). We consider sublevel set filtrations of a function \(f : \mathcal{X} \rightarrow \mathbb{R}\). The filtration is defined by increasing the parameter \(\alpha\), with \(\mathcal{X}_{ \alpha } = f^{-1} (- \infty, \alpha]\). A \(k\)-dimensional persistence diagram, \(PD_k\), is a multi-set of points in \(\mathbb{R}^2\). Each point, \((b, d)\) represents a \(k\)-dimensional topological feature which appears when \(\alpha = b\) and disappears when \(\alpha = d\). These are called the the birth time and death time respectively. Alternatively, we can view the persistence diagram as a map from a filtration to a set of points in \(\mathbb{R}^2\):
\[PD_{k} : (\mathcal{X}, f) \rightarrow \{ b_i, d_i \}_{i \in \mathcal{I}_k}\]As a notational convenience, we assume that the indexing of the points is by decreasing lifetimes, i.e. \(d_i - b_i \geq d_j - b_j\) for \(i>j\). An intuitive way to understand this machinery is to consider a filtration where simplices are added one at a time. It is a standard but non-obvious result that a \(k\)-dimensional simplex either creates a \(k\)-dimensional feature or destroys a \((k-1)\)-dimensional feature. The persistence diagram captures the pairing of these events which are represented by a pair of simplices \((\sigma, \tau)\), where \(b=f(\sigma)\) and \(d=f(\tau)\). This allows us to define an inverse map:
\[\pi_{f}(k) : \{ b_i, d_i \}_{i \in \mathcal{I}_k} \rightarrow (\sigma, \tau)\]As persistence diagrams are a collection of points in \(\mathbb{R}^2\), there are many notions of distances between diagrams and loss functions on diagrams which depend on the points. We will use loss functions that can be expressed in terms of three parameters:
\[\mathcal{E}(p,q,i_0; PD) = \sum_{i=i_0}^{\infty} \mid d_i-b_i\mid^p (\frac{d_i+b_i}{2})^q\]We sum over lifetimes beginning with the \(i_0\) most persistent point in the diagram. For example, if \(i_0 = 2\), we consider all but the most persistent class. We also use the Wasserstein distance between diagrams – this is defined as the optimal transport distance between the points of the two diagrams. One technicality is that the two diagrams may have different cardinalities, which is why points may be mapped to the diagonal.
We use two different types of filtrations: (1) a sub/superlevel set filtration where a function is defined on a fixed simplicial complex \(\mathcal{X}\) (Check out Figure 5), and (2) a distance-based filtration whose input are points embedded in some ambient space. We refer to (1) as level set persistence. As an example, we consider images where superlevel set filtrations are more natural. The underlying complex is the collection of pixels and the function is given by the pixel values, i.e. the superlevel set are all pixels whose value is greater than some \(\alpha\). If we represent each pixel by a vertex and triangulate \(\mathbb{R}^2\), the value of a simplex is given by the minimum of pixel values of vertices in the simplex. This defines a map \(\omega_{ls}(\sigma) =\mathrm{argmin}_{v\in\sigma} f(v)\) from each simplex to a vertex/pixel. Composing with \(\pi_f\), we obtain a map from a point in the diagram to a pair of pixels – evaluating the gradients at these pixels gives the gradient with respect to the diagram via the chain rule.
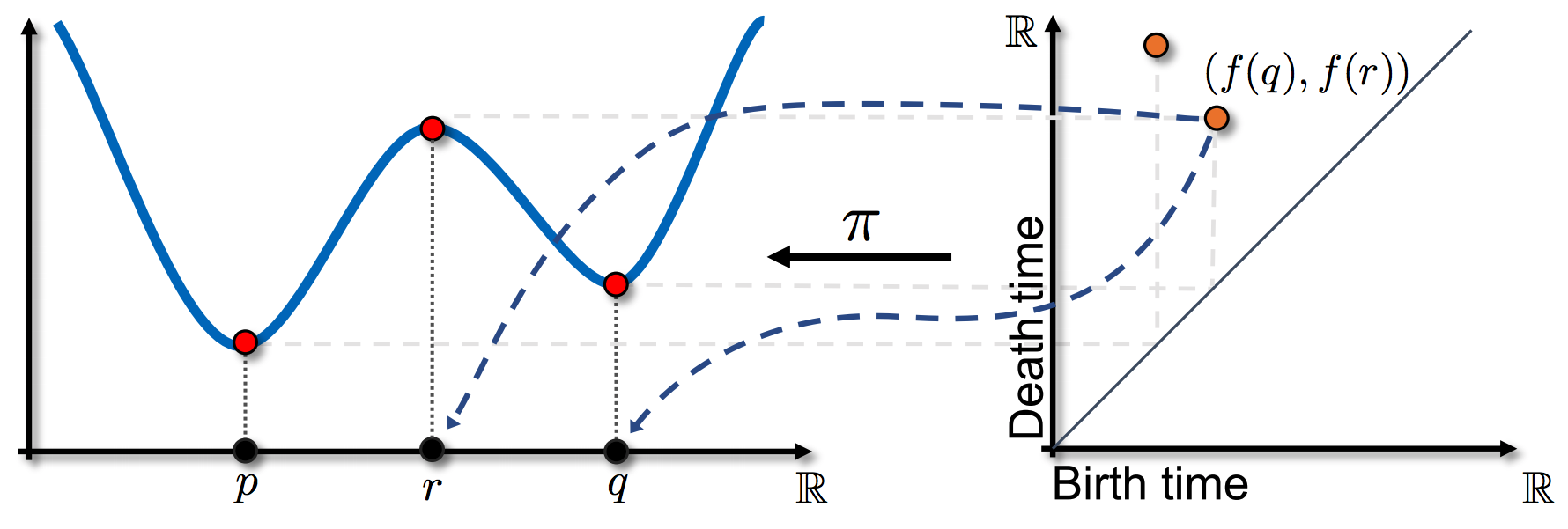
Figure 5: A one dimensional example of a persistence diagram and the inverse map \(\pi\). The function on the left has critical points at points \(p\), \(r\) and \(q\). The local minima create components in the sub-level sets and so represent birth times (\(x\)-axis), while the maxima kills one of the components (the younger one) and so is a death time (\(y\)-axis). The inverse map for a point in the diagram returns the corresponding critical points/simplicies.
In our other scenario, the input consists of points in \(\mathbf{R}^d\). One construction for this situation is the Rips filtration, \(\mathcal{R}_\alpha\). A Vietoris-Rips complex is constructed in two steps. First, connect all pairs of points \((x,y)\) if \(\mid \mid x-y \mid \mid < \alpha\). Then take the resulting graph and construct the clique complex by filling in all possible simplices, which correspond to cliques in the graph. In this setting, the filtration function is defined as \(f(\sigma) = \max_{(v,w)\in\sigma} \mid \mid v-w \mid \mid\) and the corresponding inverse map is \(\omega_{\mathcal{R}} (\sigma) = \mathrm{argmax}_{(v,w)\in\sigma} \mid \mid v-w \mid \mid\). This relies on the points being embedded – extending this definition to a general metric space would require additional work. Again composing with \(\pi_f\) gives potentially four points and the gradient can be evaluated at those four points. The Rips filtration can often become too large to compute efficiently. Rather than connect all pairs of points which are sufficiently close, we take as the graph a subset of the Delaunay graph. We refer to this as the weak Alpha filtration. With the maps defined the derivation of the gradient is straightforward application of the chain rule.
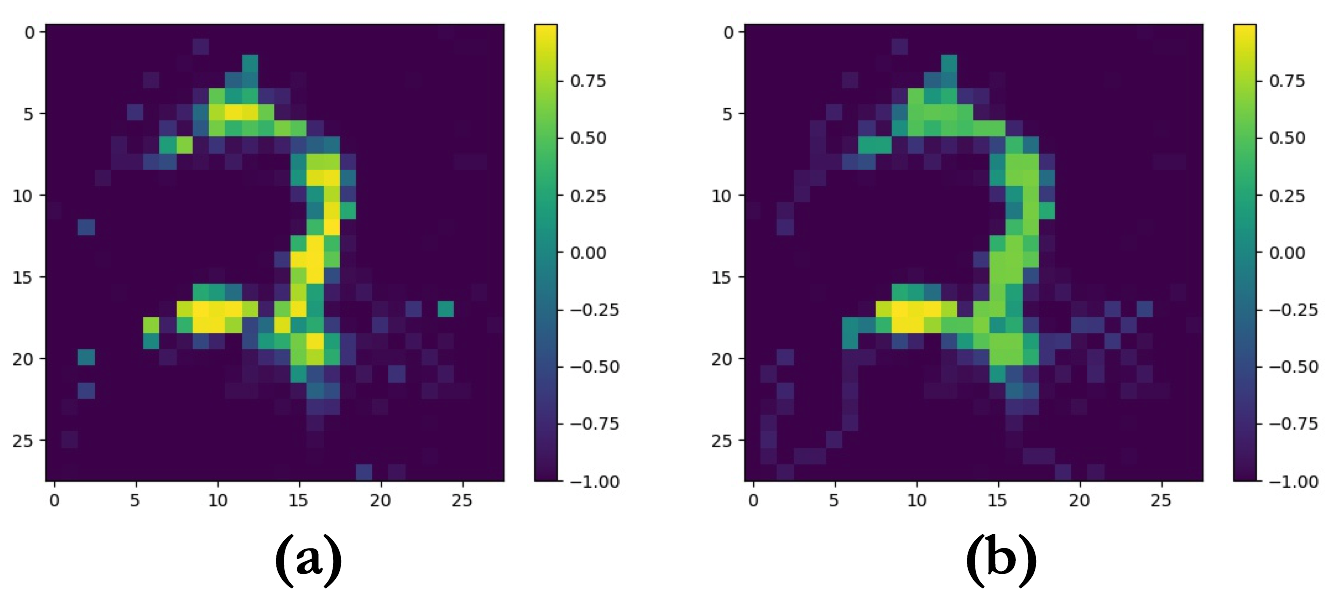
For example, in Figure 4, we used weak Alpha filtration with loss functions (a): \(- \mathcal{E}(2,0,2; PD_0)\), (b): \(\mathcal{E}(2,0,2; PD_0)\), (c): \(- \mathcal{E}(2,0,1; PD_1)\), (d): \(- \mathcal{E}(2,1,1; PD_1) + \mathcal{E}(2,0,2; PD_0)\), and (d): \(\mathcal{E}(2,0,1; PD_1)\). Similarly, we can use superlevel set filtration to denoise an image of a MNIST digit, where we encourage one global maximum via loss function \(\mathcal{E}(1,0,2; PD_0)\), the result can be seen below in Figure 6.
What we can do!
When it comes to machine learning, topology is not as ubiquitous as local geometry, but in almost all cases where local geometry is useful so is topology. However, topology is harder to wrap your head around. We will describe applications in three domains where our TopologyLayer makes leveraging topology easy peasy.
Topology Priors in Regularization
The following examples demonstrate how topological information can be incorporated effectively to add regularization or incorporate prior knowledge into problems. Furthermore, they demonstrate how topological information can be directly encoded, such as penalties on the number of clusters or number of maxima of a function, in a natural way that is difficult to accomplish with more traditional schemes.
Regularization is used throughout machine learning to prevent over-fitting, or to solve ill-posed problems. In a typical problem, we observe data \(\{X_i\}\) and responses \(\{y_i\}\), and we would like to fit a predictive model with parameters \(\hat{\beta}\) that will allow us to make a prediction \(\hat{y}_i = f(\hat{\beta}; X_i)\) for each observation. The quality of the model is assessed by a loss function \(\ell\), such as the mean squared error. However, many models are prone to over-fitting to training data or are ill-posed if there are more unknown parameters than observations. In both these cases, adding a regularization term \(P(\beta)\) can be beneficial. The estimated value of \(\hat{\beta}\) for the model becomes:
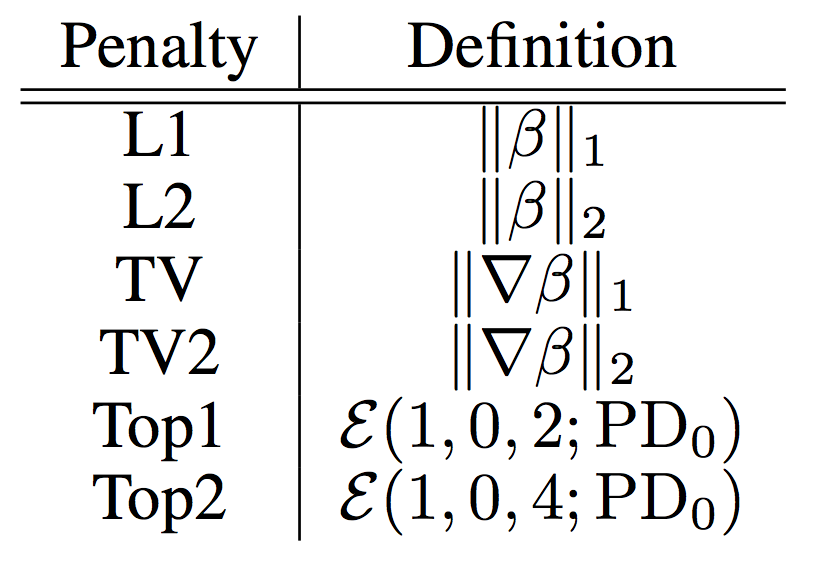
\[\hat{\beta} = argmin_{\beta} \sum_{i=1}^n \ell \big(y_i, f(\beta; X_i)\big) + \lambda P(\beta) \ \ \ \ \ \ \ \ \ \text{(1)}\]where \(\lambda\) is a free tuning parameter. We compare some common regularization to two topological regularizations Top1 and Top2 which stands for \(\mathcal{E} (1,0,2;PD_0)\) (or \(\sum_{i=2}^{\infty} \mid d_i - b_i \mid\) over \(PD_0\)) and \(\mathcal{E} (1,0,4;PD_0)\) (or \(\sum_{i=4}^{\infty} \mid d_i-b_i \mid\) over \(PD_0\)) respectively. Top1 encodes that we want to kill off all connected components other than the most persistent component, while Top2 encodes that we want to kill off all connected components other than the three most persistent components. Figure 7 shows a table and definitions of all regularization terms.
In Figures 6 and 7, we compare different regularization schemes for several different linear regression problems. Data is generated as \(y_i = X_i\beta_\ast + \epsilon_i\), where \(X_i\sim N(0,I)\), and \(\epsilon_i\sim N(0,0.05)\). \(\beta_\ast\) is a feature vector with \(p=100\) features, and an estimate \(\hat{\beta}\) is made from \(n\) samples by solving Equation (1) with the mean-squared error loss \(\ell\big(y_i, f(\beta; X_i)\big) = (y_i - X_i \beta)^2\) using different penalties, and \(\lambda\) is chosen from a logarithmically spaced grid on \([10^{-4},10^1]\) via cross-validation for each penalty. We track the mean-squared prediction error for the estimate \(\hat{\beta}\) as the number of samples is increased. We also compare to the ordinary least-squares solution, with no regularization term, although if the solution is under-determined \((n < p)\), we take the smallest 2-norm solution.
In Figure 8, the features in \(\beta_\ast\) are chosen uniformly at random from three different values. On the left, those values are \(\{-1,0,1\}\), and on the right, \(\{1, 2, 3\}\). We consider \(L_1\) and \(L_2\) penalties, as well as two topological penalties (Top1 and Top2) using a weak-alpha filtration.
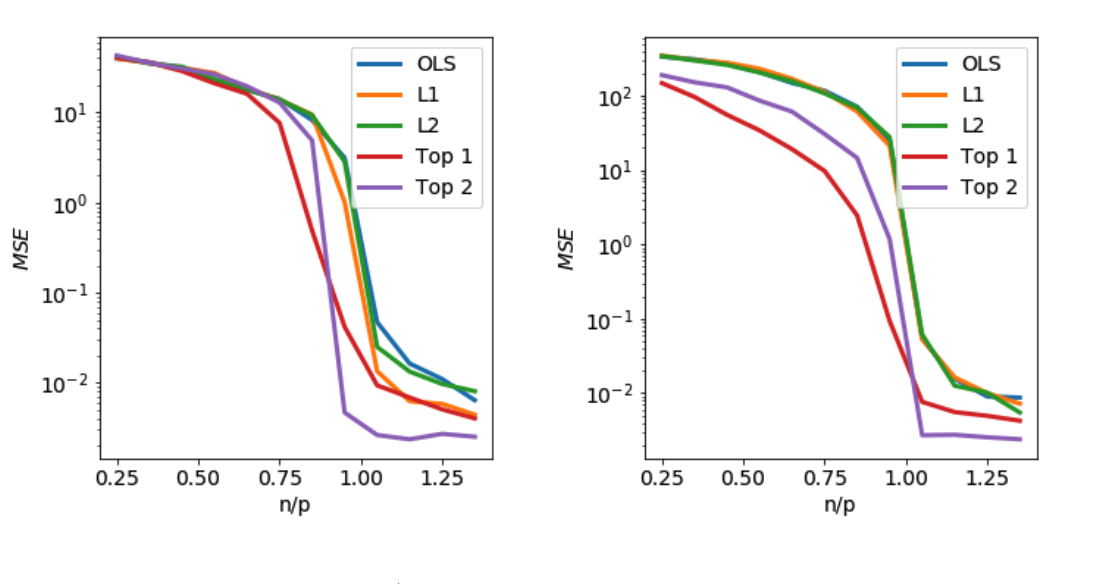
Figure 8: MSE (mean squared error) of \(\hat{\beta}\) obtained using several regularization schemes as size of training set increases. Left: entries of \(\beta_\ast\) are drawn i.i.d. from \(\{-1,0,1\}\). Right: entries of \(\beta_\ast\) are drawn i.i.d. from \(\{1,2,3\}\). \(n\): number of samples, \(p\): number of features.
In Figure 9, the features in \(\beta_\ast\) are chosen to have three local maxima when the features are given the line topology: \(\beta_\ast\) consists of three piecewise-linear sawteeth. The total variation penalty \(P(\beta) = \sum_{i=1}^p \mid \beta_{i+1} - \beta_i \mid\) and a smooth variant \(P(\beta) = (\sum_{i=1}^p \mid \beta_{i+1} - \beta_i \mid^2)^{1/2}\) are considered, as well as two topological penalties (Top1 and Top2). The parameters of the topological penalties are identical to the previous example, but the penalties are now imposed on superlevel set diagrams of \(\beta\). This means that instead of penalizing the number of clusters in the weights of \(\beta\), we now penalize the number of local maxima.
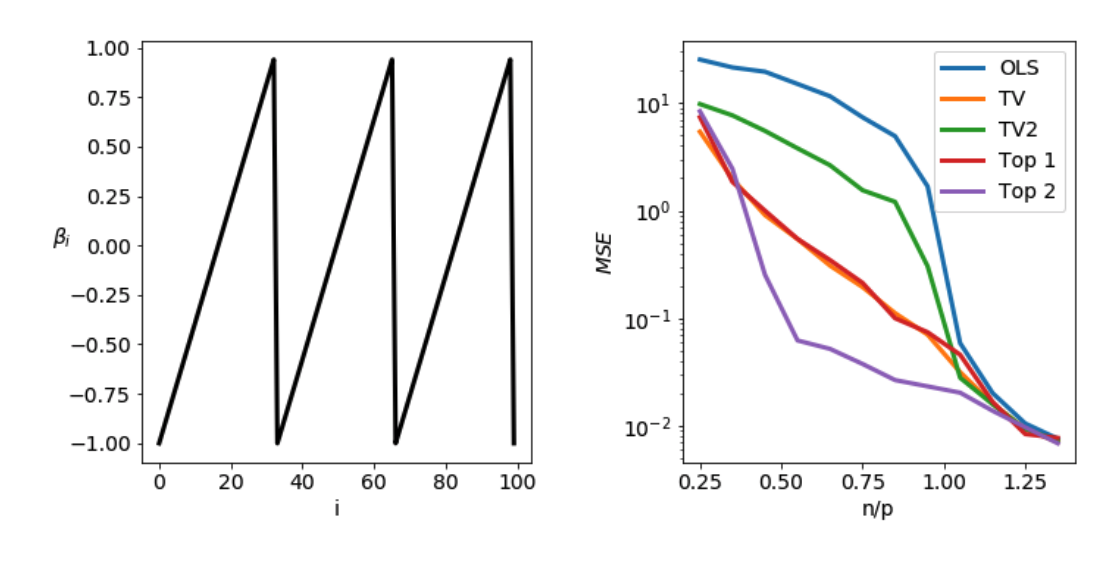
Figure 9: Sawtooth \(\beta_\ast\). MSE (mean squared error) of linear prediction using \(\hat{\beta}\) obtained from several regularization schemes as size of training set increases. \(n\): number of samples, \(p\): number of features.
These examples show that useful topological priors exist already in basic machine learning settings and how our TopologyLayer can easily incorporate such priors to good use.
Topology Priors for Generative Models
We now use the same topological priors to improve the quality of a deep generative neural network. Specifically, we want to improve its topological fidelity and the right number of local maxima. We start with a Baseline-Generator, pre-trained in a GAN-setup on MNIST, and by training it for a few iterations (only 50 batch-iterations to be exact) with a topological loss, we arrive at an improved Topology-Generator. We use the same loss, \(\mathcal{E}(1,0,2; PD_0)\) (topology loss), as in the MNIST digit denoising in Figure 6. The setup looks as in Figure 10 and the qualitative results can be seen in Figure 11.
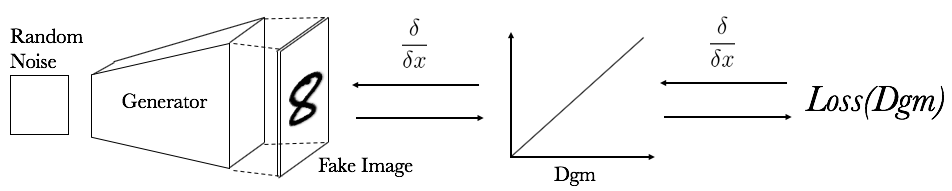
Figure 10: Setup for training generator with topology loss. \(Loss(Dgm) = \mathcal{E}(1,0,2; PD_0) =\) \(\sum_{i=2}^{\infty} \mid d_i - b_i \mid\) over \(PD_0\).

The topology loss allows the generator to learn in only 50 batch iterations to produce images with a single connected component and the difference is visually significant. Furthermore, consider the linear interpolation in the latent space of the Baseline-Generator and Topology-Generator in Figure 12. The two different cases behave very differently with respect to the topology. The Baseline-Generator interpolates by letting a disconnected components appear and grow. The Topology-Generator tries to interpolate by deforming the number without creating disconnected components. This might be most obvious in the interpolation from ‘1’ to ‘4’ (Figure 12, right hand side) where the appended structure of the ‘4’ appears as a disconnected component in the baseline but grows out continuously from the “1” in the topology-aware case.
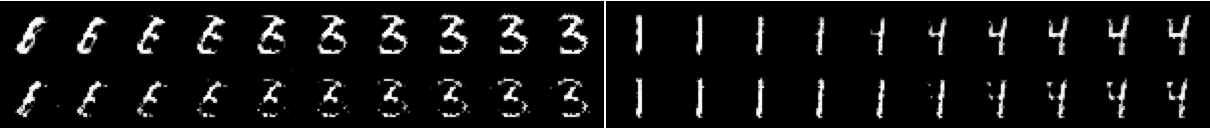
We also quantitatively compare the Baseline-Generator and Topology-Generator to further investigate if any improvements have been made. We use the Minimal Matching Distance (MMD) and Coverage metric as advocated by 1 as well as the Inception score2 (a convolutional neural network with 99% test accuracy on MNIST was used instead of the Inception model). The results can be seen in Figure 13. MMD-Wass and COV-Wass use the same procedure as MMD-L2 and COV-L2 but instead of the L2 distance between images, the 1-Wasserstein distance between the 0-dimensional persistence diagrams of the images was used. The Topology-Generator shows improvements on all but one of these metrics.

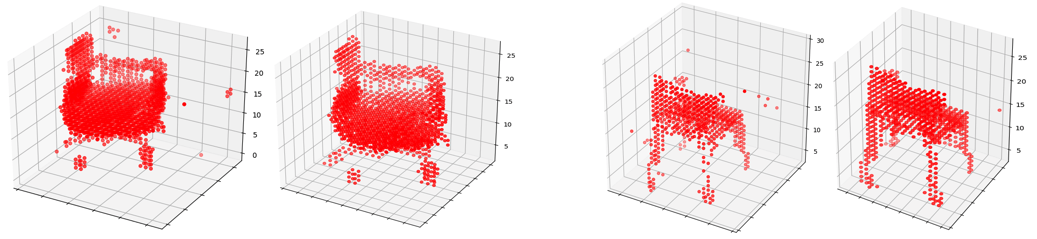
We extend this superlevel set filtration to 3D data in the form of voxel grids. As before, a baseline generator is obtained by training a GAN to generate voxel shapes as 3 and its output after 1,000 epochs (or 333,000 batch iterations) can be seen in Figure 14 as the left hand members in each of the two pairs. The result of training with the topology loss (same as for images) for 20 batch iterations can be seen in Figure 14 as the right hand members in each of the two pairs. We claim no improvements on general metrics in this case but note that the generator is able to learn to generate output with far fewer connected components.
Topological Adversarial Attacks
Our topological layer may also be placed at the beginning of a deep network. In contrast to other approaches that use persistence features for deep learning, we can use the fact that our input layer is differentiable to perform adversarial attacks, i.e. we want to cause a trained neural network to misclassify input whose class to us is fairly obvious, and we do this by backpropagating from the predictions back to the input image, which is known as a gradient attack.
Since standard super-level set persistence is insufficient to classify MNIST digits, we include the orientation and direction information by computing the persistent homology during 8 directional sweeps. The model (TopModel) trained to classify the digits based on these topological features achieved 80-85% accuracy. Next we performed gradient attack 4 to change the classification of the digit to another target class. We observe that it is harder to train adversarial images compared to CNNs and MLPs. The results are shown in Figure 15. A red outline indicates that the attack was successful. When the attack was conducted on 1,000 images, to retarget to a random class, it had 100% success rate on MLP and CNN models and 25.2% success rate on the TopModel.

Figure 15: Topological adversarial attack on TopModel, MLPModel and CNNModel. Each \((i,j)\)-cell with \(i,j \in \{0, 1, \cdots, 9\}\) represents an attack on an image with label \(i\) to be classified with label \(j\). Red outline indicates successful attack.
When the adversarial attacks succeed the results sometimes offer insight as to how the model classifies each digit. For example in Figure 16, the left image is the original image of the digit 4, the right was trained to be classified as an 8; notice that two small holes at the top and bottom were sufficient to misclassify the digit. Several instances of the topological attacks provide similar interpretation. Attacks on MLP and CNN are qualitatively different, but further work is needed to gauge the extent and utility of such distinctions.
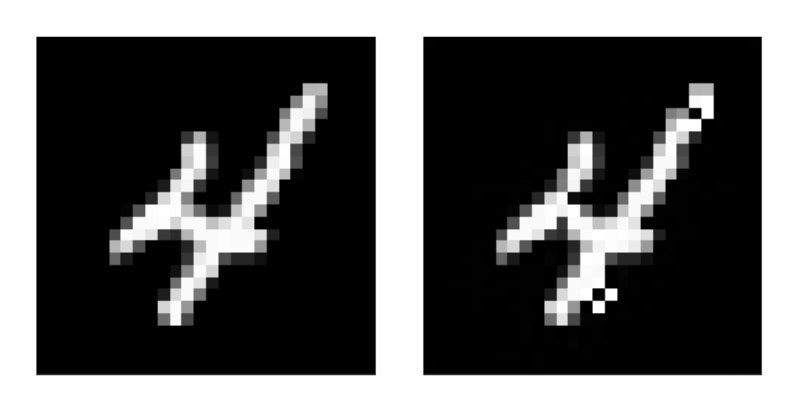
Conclusion
In this post we have introduced a general framework for incorporating global geometry in the form of topology into machine learning domains. In each of the examples we showcase how global geometry, through our TopologyLayer, can be used in cases where local geometry is today usually solely relied upon. We present both quantitative and qualitative advantages that can be achieved by incorporating topology into these domains and hope this will inspire the machine learning community at large to embrace global geometry and topology.
This work only scratches the surface of the possible directions leveraging the differentiable properties of persistence. Without doubt such work will tackle problems beyond those we have presented here. Such work could include encouraging topological structure in intermediate activations of deep neural networks or using the layer in the middle of deep networks to extract persistence features where they may be more useful. However, many of the applications we have presented here also deserve further focus. For example, topological regularization, including the penalties we have presented, may have interesting theoretical properties, or closed form solutions. Furthermore, training autoencoders with distances such as the bottleneck or Wasserstein distance between persistence features might produce stronger results than the functions considered here. Finally, it might prove useful to use topological features to train deep networks that are more robust to adversarial attacks – however, as we show this will require additional work.
Topology, in contrast to local geometry, is generally underexploited in machine learning, but changing this could benefit the discipline. Go ahead and install the TopologyLayer, play around with it, and see for yourself all kind of cool things it can do.
Post based on preprint: A Topology Layer for Machine Learning by Rickard Brüel-Gabrielsson, Bradley J. Nelson, Anjan Dwaraknath, Primoz Skraba, Leonidas J. Guibas, and Gunnar Carlsson.
Work supported by Altor Equity Partners AB through Unbox AI (unboxai.org) and by the US Department of Energy, Contract DE-AC02-76SF00515.
-
Panos Achlioptas, Olga Diamanti, Ioannis Mitliagkas, and Leonidas Guibas. Learning representations and generative models for 3D point clouds. In Proceedings of the 35th International Conference on Machine Learning, volume 80 of Proceedings of Machine Learning Research, pages 40–49, Stockholmsmässan, Stockholm Sweden, 10–15 Jul 2018. ↩
-
Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. Improved techniques for training gans. In Proceedings of the 30th International Conference on Neural Information Processing Systems, NIPS’16, pages 2234–2242, 2016. ↩
-
Jiajun Wu, Chengkai Zhang, Tianfan Xue, Bill Freeman, and Josh Tenenbaum. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. In Advances in neural information processing systems, pages 82–90, 2016. ↩
-
Ian Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In International Conference on Learning Representations, 2015. ↩