

Next: Collineations
Up: The Projective Plane
Previous: Conics
A surprising property of conics is that every circle intersects the
ideal line, W=0, at two fixed points. To see this, note that
a circle is a conic with all off-diagonal elements (c12, c13,
and c23) set to zero and all diagonal elements equal:
X2 + Y2 + W2 = 0,
which therefore intersects the ideal line W=0 at
X2 + Y2 = 0.
This equation has two complex roots, known as the
absolute points:
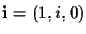 and
and
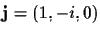 .
(Although we have, for simplicity, assumed that
homogeneous coordinates are real, they can
in general be the elements of
any commutative field in which
.
(Although we have, for simplicity, assumed that
homogeneous coordinates are real, they can
in general be the elements of
any commutative field in which 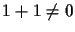 [1, p. 112].)
It will be shown in the next two
subsections that the absolute points remain invariant under similarity
transformations, which makes them useful for determining the
angle between two lines.
[1, p. 112].)
It will be shown in the next two
subsections that the absolute points remain invariant under similarity
transformations, which makes them useful for determining the
angle between two lines.
Stanley Birchfield
1998-04-23