Suppose we have a stereo pair of cameras viewing a point
![]() in the world which
projects onto the two image planes at
in the world which
projects onto the two image planes at
![]() and
and
![]() (Since we are dealing
with homogeneous coordinates,
(Since we are dealing
with homogeneous coordinates,
![]() is
is
![]() ,
and
,
and
![]() and
and
![]() are each
are each
![]() ). If we assume the cameras are calibrated, then
). If we assume the cameras are calibrated, then
![]() and
and
![]() are given
in normalized coordinates, that is, each is given with respect to its
camera's coordinate frame. The epipolar constraint says that
the vector from the first camera's optical center to the first imaged
point, the vector from the second optical center to the second imaged
point, and the vector from one optical center to the other are all
coplanar. In normalized coordinates, this constraint can be expressed
simply as
are given
in normalized coordinates, that is, each is given with respect to its
camera's coordinate frame. The epipolar constraint says that
the vector from the first camera's optical center to the first imaged
point, the vector from the second optical center to the second imaged
point, and the vector from one optical center to the other are all
coplanar. In normalized coordinates, this constraint can be expressed
simply as
Now suppose the cameras are uncalibrated. Then the matrices
A1 and A2 (from (4)) containing the internal
parameters of the two cameras
are needed to transform the normalized coordinates into pixel coordinates:
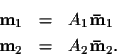
Thus both the Essential and Fundamental matrices completely describe the geometric relationship between corresponding points of a stereo pair of cameras. The only difference between the two is that the former deals with calibrated cameras, while the latter deals with uncalibrated cameras. The Essential matrix contains five parameters (three for rotation and two for the direction of translation -- the magnitude of translation cannot be recovered due to the depth/speed ambiguity) and has two constraints: (1) its determinant is zero, and (2) its two non-zero singular values are equal. The Fundamental matrix contains seven parameters (two for each of the epipoles and three for the homography between the two pencils of epipolar lines) and its rank is always two [4].
There are several other ways to derive the Essential and Fundamental Matrices, each of which presents a little more insight into their nature. In the next few subsections, we will look at these methods and then summarize our findings.