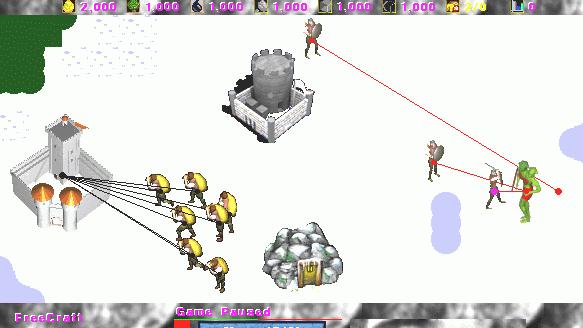

Freecraft strategic task with 9 peasants, 3 footmen and 1 enemy.
In the strategic domain, the goal is to kill a strong enemy. Our player starts with a few peasants, who can collect gold or wood, or attempt to build a barrack, which requires both gold and wood. All resources are consumed after each Build action. With a barrack and gold, the player can train a footman. The footmen can choose to attack the enemy. When attacked, the enemy loses ``health points'', but fights back and may kill the footmen.
There are seven classes of objects in the world: peasants, builder (a subclass of peasant which can build barracks), footmen, enemies, barracks, gold, and wood. We begin with one builder and a variable number of peasants, without any resources (gold or wood), and one strong enemy in the distance. Both the builder and the regular peasants have actions to wait, collect gold, and collect wood.
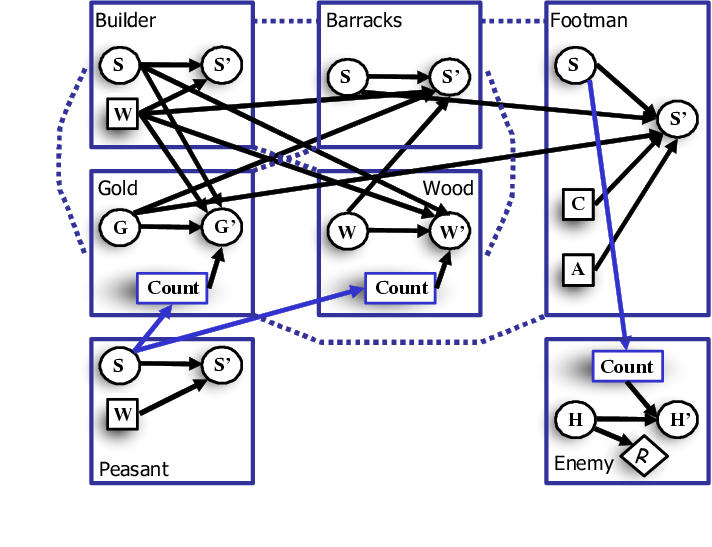
RMDP schema for Freecraft tactical domain.
Mining for gold or harvesting wood during a time step gives us some probability of increasing the amount of the resource in the next time step. This probability depends on the number of peasants performing the task. Further, the builder can attempt to build a barrack. After the build action is taken a barrack is built with high probability, if enough gold and wood resources are present. Both the gold and the wood are spent when the barrack is constructed. We begin with no living footmen, but with a given number of "available" footmen. We can attempt to create a footmen at any time, but will fail unless we have both a barrack and enough gold. Once a footman is alive, it can either wait or attack the enemy. If it waits, it is safe but will not hurt the enemy. Conversely, if it attacks it may injure the enemy, but has a probability of dying as the enemy fights back. In an attack, the number of "health points" lost by the enemy depend on the number of footmen attacking it.
To encourage coordination, every regular peasant is related to the builder, in a star-like pattern. Furthermore, as in the tactical model, every footman had a "buddy" in a ring. In addition, objects have relations to the gold, wood, barrack, and enemy. The scope of our local value function included triples between related objects.
We solved a model with 2 peasants (a builder and a regular peasant), 1 barrack, 2 footmen, and an enemy. The resulting policy is quite interesting. Initially, the peasants begin gathering gold. Once they have enough to create the barrack, they gather the necessary wood. They build the barrack, then return to get the gold needed to build footmen. Rather than attacking the enemy with the first footman, the policy has this footman wait until we are able to build the second footman. Then, the two attack the enemy together. The stronger enemy is able to kill both footmen, but not without taking significant damage. When the next footman is trained, it immediately attacks rather than wait for the second one to be created. The now injured enemy is unable to hold up, and the footman wins the battle.
Although it would be intractable to plan for significantly larger worlds, action selection can be performed efficiently. Thus, we used our generalized value function to tackle a world with 9 peasants and 3 footmen, without replanning. The much larger force of peasants demonstrates the same coordination, rapidly collecting enough gold and wood to build the barrack, then footmen. Interestingly, rather than attacking with 2 footmen, the policy now waits for 3 to be trained before attacking. The 3 footmen manage to kill the enemy quickly, only losing one footman in the process.
We have created a model which simulates a the basic strategic aspect of Freecraft with approximately 106 joint state-action pairs. We find an approximation of the value function that defines a policy which efficiently kills the enemy. Further, we have successfully generalized from this problem to the larger 9 peasants and 3 footmen problem, which contains over 1013 state-action pairs.
We planned in a model with 2 peasants (a builder and a regular peasant), 1 barrack, 2 footmen, and an enemy. Note that only after both footmen are built, they start attacking the enemy. Nonetheless, both are killed by the stronger enemy. However, as the enemy becomes weak after this attack, in the next round, only one footman is sent to attack it.
We generalized to a model with 9 peasants (a builder and 8 regular peasants), 1 barrack, 3 footmen, and an enemy. Here our policy waits for the 3 footmen to be built before attacking. They are able to kill the enemy, and only one footman is lost.