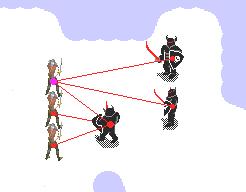

Freecraft tactical task with 3 footmen against 3 enemies.
In the tactical model, the goal is to take out an opposing enemy force with an equivalent number (n) of units. Each footman and enemy can move around and attack any member of the opposing force. The goal is to coordinate the movements and attacks of one's force to defeat the other. The enemies are controlled using Freecraft's hand-built strategy.
Our model approximates Freecraft as follows. Each footman and enemy "health points" are discretized into 5 values, which decrease with some probability when attacked. If multiple footmen attack an enemy, they each have an independent chance to decrement the enemy's health points, and may jointly decrement this counter by multiple points per time step. When an enemy or footman's health points reach zero, it is dead and can no longer attack. Unlike Freecraft, however, the enemies in our simplified model each have a unique and fixed target (e.g., enemy1 will only attack footman1), while the footmen can switch their targets at each time step. In Freecraft, the enemies can actually switch their target. Furthermore, our model does not incorporate the spatial characteristics of Freecraft. Therefore our footmen switch targets immediately.
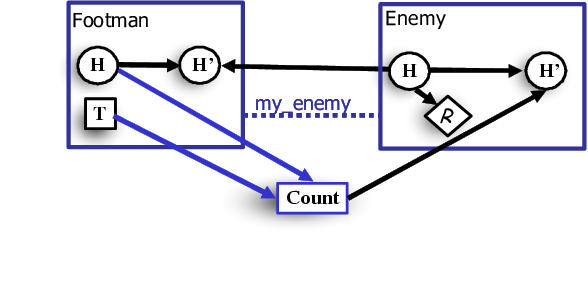
RMDP schema for Freecraft tactical domain.
Footman and enemy health points comprise
the set of state variables; footman target selections are modeled
as actions performed at each time step. The domain of each
action is the set of enemies in a particular instantiation of the RMDP. A footman's health in the next time step depends on
its current health and the health
of its enemy. An enemy's health depends on its prior
health and an aggregator which counts the number of living footmen
who had selected that enemy as their target. A reward is received
for each dead enemy at each time step.
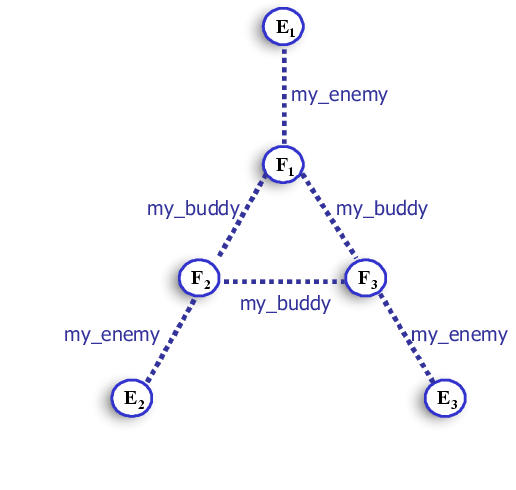
Coordination structure in Freecraft tactical domain.
Each footman is related to another footman (its "buddy") in a ring structure (such that footman i is linked to footman ((i+1)%n) and to its enemy. We approximated the value function using local value functions over triples of related variables. In particular, we used triples over each footman's health, its enemy's health, and its buddy's health; and over each footman's health, its enemy's health, and its buddy's enemy's health.
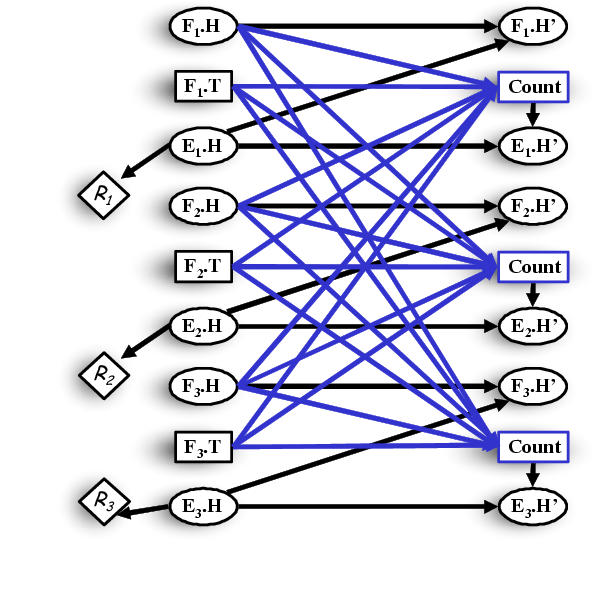
Instantiation of RMDP schema with 3 footmen and 3 enemies for tactical model.
We solved this model for n=3
and used the resulting class-level weights to generalize to n=4
and n=5.In Monte Carlo simulations of the model, the learned and generalized
policies perform very well and exhibit interesting coordination. Footmen concentrate their efforts
on single enemies; divide again when
the enemy has become weakened and only a few footmen are required to
finish it; select new targets on the basis of the threat they pose
to particular footmen (that is, the current health of the footmen); and
even abandon severely weakened footmen for dead, reasoning that they
will be unable to save them and that their enemies, who are unable
to select new targets, pose no further threat.
In Freecraft, our policies perform
well for n=3. The coordination exhibited in Monte Carlo simulation
translates well to Freecraft. Our policy defeats Freecraft's force
with two surviving footmen. The coordination strategy generalizes effectively to n=4.For example, all footmen initially focus
on a single enemy, and one by one find new targets as the enemy is weakened. Our policy succeeds again with one
surviving (but completely healthy)
footman. However, the generalized policy performs poorly for
n=5, despite its superior performance with respect to the model. Indeed, our
model becomes inadequate as n increases, because
it does not take into account the distances over which footmen must
move to attack a new target, or the possibility that enemies or even other
footmen may obstruct their paths. In Freecraft, our footmen become
separated from each other and are unable to attack obstructed targets simultaneously.
The result is a close contest, but Freecraft ultimately wins.
For best visualization of these movies, please select the full screen feature in your player.
We planned in a model with 3 footmen and 3 enemies. Here the footmen coordinate and are able to kill the enemies, losing only one footman in the process.
We generalized our value function to a problem with 4 footmen and 4 enemies. The coordination strategy generalizes very effectively. Note in the video that at first, all footmen attack one enemy. As this enemy weakens, they coordinate, decreasing the number of footmen on this enemy, until only one footman is left. This footman finishes off the enemy, and moves on to the next one.
We then generalized our value function to a problem with 5 footmen and 5 enemies. Here, the footmen also demonstrated interesting coordination. For example, in the beginning 4 footmen attack one enemy and 1 attacks another. Our model says that the probability of killing an enemy with more than 4 footmen is the same as the one with 4 footmen. Although we never planned in a problem with 5 footmen, our generalization captures this characteristic of the model. Unfortunately, at this point, we do not take into account the position of the units. In this example, one unit spends a lot of time trying to reach an enemy. This inefficient causes our policy to lose to Freecraft's one in a close battle.