Manipulator Planning and Obstacle Avoidance Using Genetic Algorithm

Abstract and Motivation

This work has been done towards my B-Tech Project in Manipulator Planning. It is about robot path planning for redundant parallel plane serial manipulator using genetic algorithm Here I have made use of interesting chapters taught in the course: "ME 767: Evolutionary Algorithms in Engineering Design" taken by Dr. Kalyanmoy Deb, Professor, Mechanical, IIT Kanpur.

While experimenting with the "Potential Field Approach" in Manipulator Planning, we constantly felt the need of a robust Path Planning and Obstacle Avoidance algorithm. In the "Potential Field Approach", the Manipulator arm was constantly vibrating near the obstacle. We realized that it would be very impractical to implement "Potential Field Approach" for our B-Tech Project. Demonstration of robustness of Genetic Algorithm in solving various engineering problems by Dr. Deb in the lectures of Genetic Algorithm, encouraged us to use Genetic Algorithm for Path Planning and Obstacle Avoidance. Morever it gave us a chance of doing something new and innovative.

Approach

• Problem representation: In Genetic Algorithm, a pool/population of strings is processed many times. Each member string in the pool/population represents a possible solution. Some strings represent infeasible solutions, while some represent good solution. Eventually after many processing the population converges to the best possible solution, i.e. only the copies of good solutions are left and bad ones are eliminated.
  In our case of 4 DOF freedom manipulator, a string would represent the increments to the four joint angles; e.g. at a gives position, the best string would give the best incremental values for the four joints. "Best incremental values" refer to those increment values to the joint angles which would avoid obstacles and move towards the goal.

  Thus a string(S) would look like: { d(theta1), d(theta2), d(theta3), d(theta4) } .

  Since here we directly coding the string a set of four real numbers, the process would be called "Real-coded Genetic Algorithm".

  If theta = { theta1, theta2, theta3, theta4 } represents the current state (joint angles) of the manipulator arm, then for this state, it required to find a (S) which moves the manipulator towards the goal by a small amount avoiding the obstacle. Thus reaching the goal involves a number of steps and in each step we have to find the best (S).

• Finding the best string (S) at each step: In this step, initially a large random population of such strings is generated. After this follows a number of Genetic Algorithm generations. In each run strings representing bad solutions are eliminated and strings representing good solutions get multiplies. After a certain number of generations the population converges to a state where majority of the string represent a single solution which is considered to be best.
  The decision whether the string is good or bad is decided by the fact whether the string solution would lead the manipulator into obstacles or not and whether the manipulator is progressing towards the goal or not. Also a maximum increment or decrement of five degrees in joint angles is allowed. Strings giving increment more than this or decrement less than this are considered to be bad.
  Based on such decisions each string in the population is assigned a fitness value. Good solutions will have high fitness value and bad solution would have low fitness value. Thus a string with a high fitness value would indicate that the manipulator is moving towards the goal without violating any constraints (like keeping out of the obstacle and keeping within the maximum allowed joint angle change at a time). In the language of Genetic Algorithm, we penalize the solution (reduce its fitness function by factors proportional to the violation size) if it is violating the constraints.
  Two Genetic Algorithm operators: Reproduction and Crossover operate on the population in each generation. In Reproduction, good solutions (strings having high fitness value) are assigned more copies and bad solutions (strings having low fitness value) get eliminated. The crossover operator (real coded SBX crossover operator) generates pair of new strings (called children) from a pair of strings (called parents) from the population. Thus the crossover operator introduces new individual strings to the population. The combination of the two operator finds the best string.
  In our case ten generations (with a population size of 100) were sufficient to find the optimal solution.
  After finding the best solution we update the joint angles with the values given by the best string, we continue this process until we reach the goal.
  

Tests & Results

• The following is the case of two obstacles. The manipulator starts from the lower end of the left obstacle and makes way to top of right obstacle through a quite constricted gap. This we couldn't achieve using traditional "Potential Field Approach", as the repulsion from the boundaries in the gap did not allow the manipulator to enter.

  





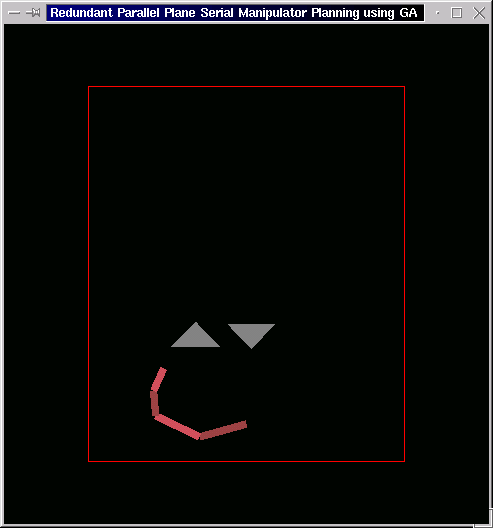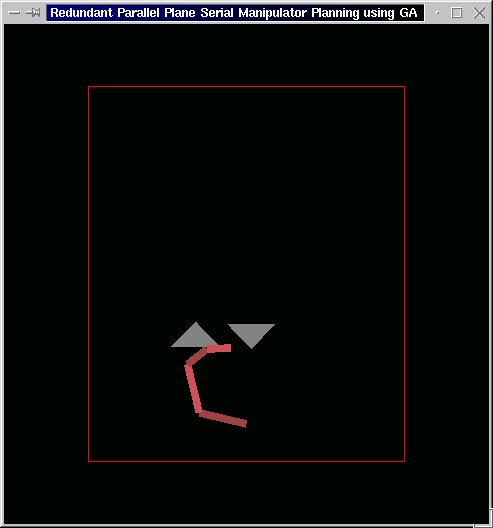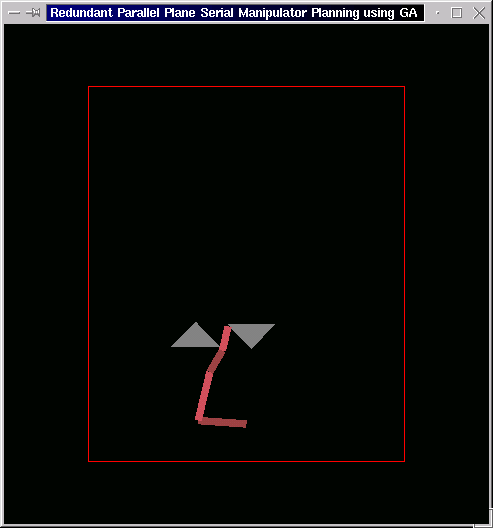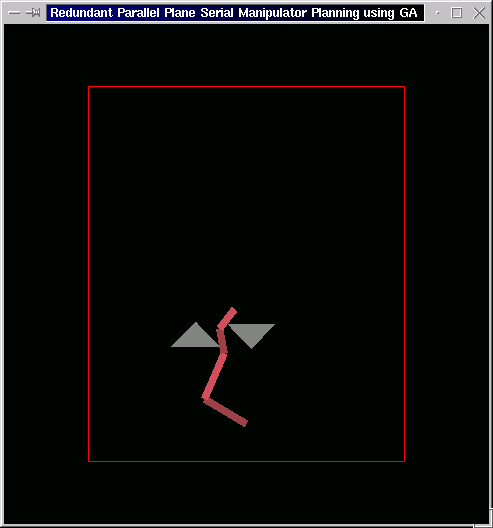
• The following is the case of three obstacles. The end-effector starts from the left side of the leftmost obstacle and moves through the "gate" between the two right obstacles to its goal at the right of the bottom-right obstacle.

  





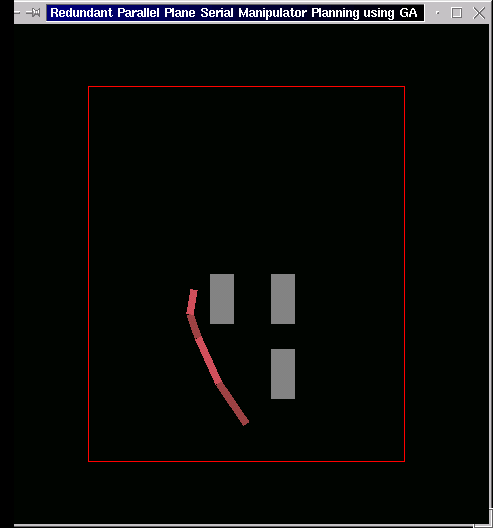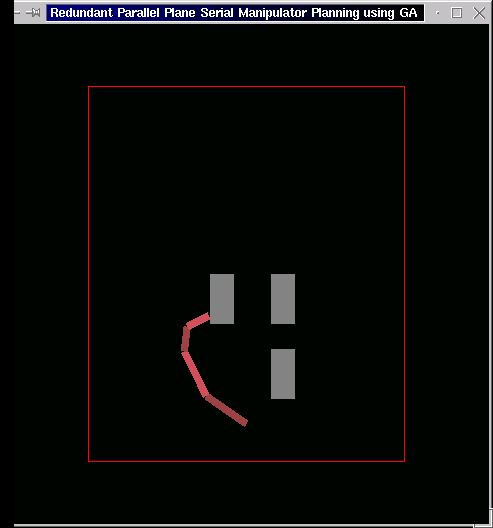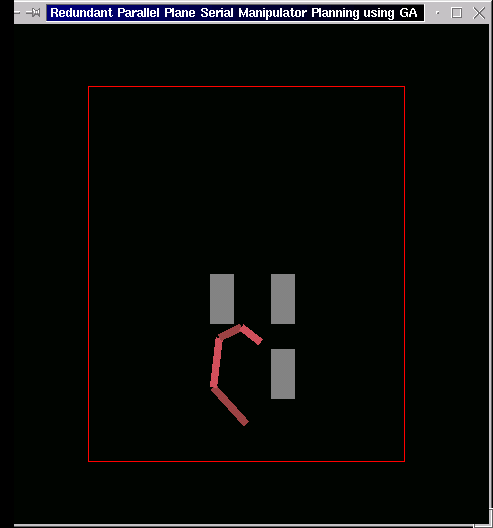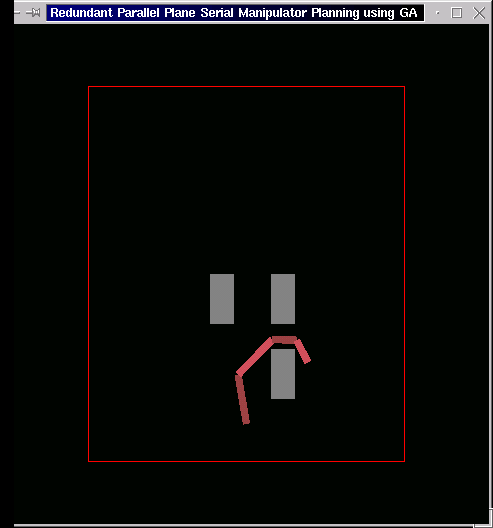
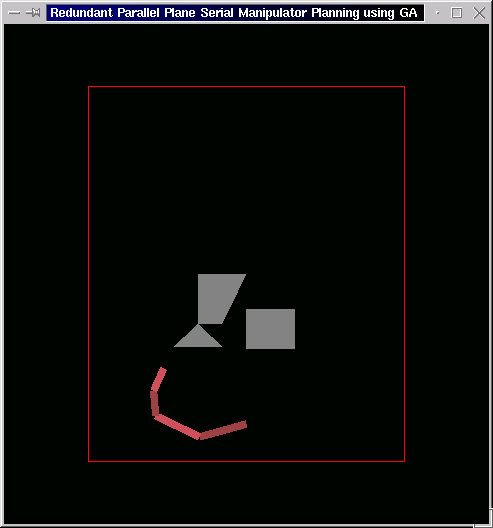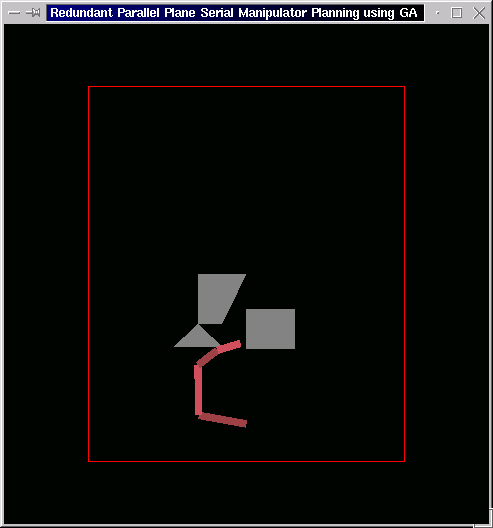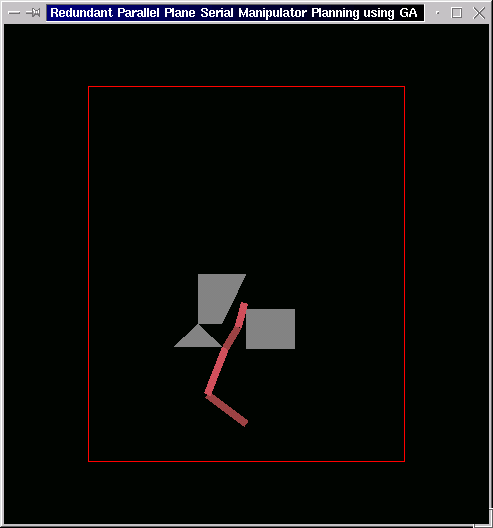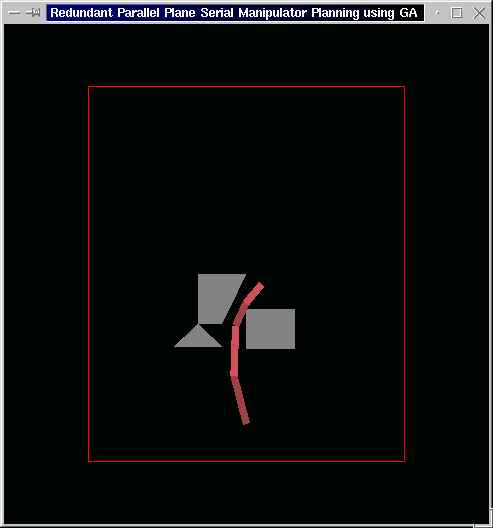
• The following is again the case of three obstacles with more constricted gap. The end effector here starts from the lower end of the triangular obstacle and moves towards the goal at the top of the square obstacle.

  

---

Conclusion

This approach is free from the major problems of "Potential Field approach" like vibration of the manipulator arm near obstacles. In the first example shown above the end-effector is making its way through a narrow and constricted region, which we could not achieve from "Potential Field approach". Inverse Kinematics is the byproduct of this approach; by modifying the source code, one can easily use it for trajectory planning in cartesian space without using Inverse Kinematics.

---

References

• Genetic Algorithm in Search Optimization and Machine learning,
  - D. E. Goldberg.
• Simulated Binary Crossover for Continuous Search Space,
  - K. Deb and R. B. Agarwal.

---

mitul@iitk.ac.in

Home Page & Other Works