


Next: Non normalized Redundancy
Up: suppl_html
Previous: Summary of MI levels
A frequently used measure of synergy and redundancy in the literature
is the difference between the information conveyed by two cells
together and that conveyed by the two cells considered individually,
![\begin{displaymath}
\left[{I(X_1;S) + I(X_2;S)}\right] - I(X_1,X_2 ; S) \; .
\end{displaymath}](img22.png) |
(5) |
This synergy-redundancy measure can be rewritten as
![\begin{displaymath}
SR = \left[{I(X_1;S) + I(X_2;S)}\right] - I(X_1,X_2 ; S)
= I(X_1;X_2) - I(X_1;X_2\vert S) \;,
\end{displaymath}](img23.png) |
(6) |
and can be therefore interpreted as being the difference of two
non-negative terms. The first, 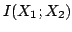 , measures between-stimuli
correlations and quantifies the stimulus induced redundancy; and the
second,
, measures between-stimuli
correlations and quantifies the stimulus induced redundancy; and the
second, 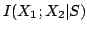 , measures within-stimulus correlations and
roughly corresponds to synergy.
, measures within-stimulus correlations and
roughly corresponds to synergy.
Figure:
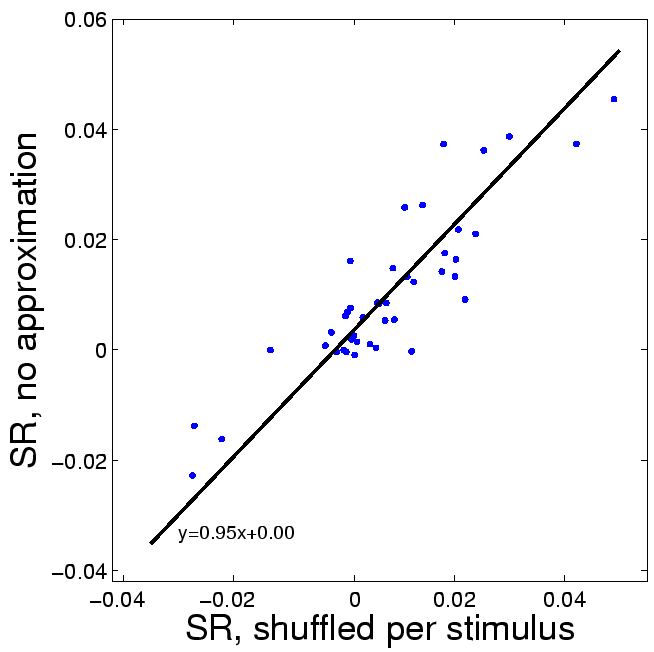
S1. Synergy-redundancy in simultaneously recorded A1
neurons. The ordinate represents the values estimated from the
actual measured distribution. On the abscissa, the calculation was
repeated while shuffling the responses of one neuron within each
stimulus separately, thus creating a stimulus-independent coupling
between the two neurons in each pair.
 |
We measured redundancy and synergy for a subset of cells that were
recorded simultaneously (39 A1 cells forming 49 simultaneously
recorded pairs) using a large number of presentation of each stimulus
(100 repeats per stimulus). This number of repeats allowed reliable
estimation of both the non conditioned information 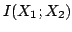 and of
the stimulus-conditioned information
and of
the stimulus-conditioned information 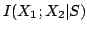 in pairs of
cells. To estimate the magnitude of the last term, we calculated SR,
and then calculated it again after a random shuffling of the responses
within each stimulus. In the limit of infinite data this shuffling
should set the conditional information to zero, but finite sampling
effects lead to distribution dependent biases
[4]. Figure S1 is a scatter plot of the
stimulus-conditioned information estimated with and without shuffling,
showing that the two are almost identical: the bi-directional
regression line (measured as the first principal component) has a
slope of 0.95, and the intercept is 0. Therefore, in this data,
stimulus dependent correlations are negligible, and the SR measure can
be well approximated using
in pairs of
cells. To estimate the magnitude of the last term, we calculated SR,
and then calculated it again after a random shuffling of the responses
within each stimulus. In the limit of infinite data this shuffling
should set the conditional information to zero, but finite sampling
effects lead to distribution dependent biases
[4]. Figure S1 is a scatter plot of the
stimulus-conditioned information estimated with and without shuffling,
showing that the two are almost identical: the bi-directional
regression line (measured as the first principal component) has a
slope of 0.95, and the intercept is 0. Therefore, in this data,
stimulus dependent correlations are negligible, and the SR measure can
be well approximated using 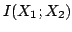 under the conditional
independence approximation.
under the conditional
independence approximation.
The use of the conditional independence approximation has considerable
practical advantages. Computing the full standard synergy-redundancy
value requires to estimate the full joint distributions of all stimuli
and responses of two or more neurons. This requires a substantially
larger number of repeats of each stimulus than is usually done for
studying the responses of single neurons. For example, with only 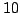 stimuli, estimating redundancy in three neurons with dynamical range
of
stimuli, estimating redundancy in three neurons with dynamical range
of 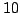 values requires at least
values requires at least 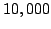 stimulus repeats, which are
extremely hard to obtain in electrophysiological experiments. With the
conditional independence approximation, the number of parameters that
are required to compute the MI depends linearly, rather than
exponentially, on the number of neurons, making MI estimation
manageable. Furthermore, using the conditional-independence
approximation allowed us to increase our sample using neuronal pairs
and triplets that were not recorded simultaneously. Finally, such
conditional independence approximations are prominent in learning
multivariate distributions and often allow more reliable estimation
with limited samples [2]. The lesson learned from this
field is that when distributions are estimated from examples, better
accuracies are often obtained when applying �incorrect� independence
approximations, since these allow more reliable estimation of the
joint distribution. In fact, the conditional independence
approximation has been used previously in neural redundancy
calculations, for precisely the above reasons, for example by
[5].
stimulus repeats, which are
extremely hard to obtain in electrophysiological experiments. With the
conditional independence approximation, the number of parameters that
are required to compute the MI depends linearly, rather than
exponentially, on the number of neurons, making MI estimation
manageable. Furthermore, using the conditional-independence
approximation allowed us to increase our sample using neuronal pairs
and triplets that were not recorded simultaneously. Finally, such
conditional independence approximations are prominent in learning
multivariate distributions and often allow more reliable estimation
with limited samples [2]. The lesson learned from this
field is that when distributions are estimated from examples, better
accuracies are often obtained when applying �incorrect� independence
approximations, since these allow more reliable estimation of the
joint distribution. In fact, the conditional independence
approximation has been used previously in neural redundancy
calculations, for precisely the above reasons, for example by
[5].



Next: Non normalized Redundancy
Up: suppl_html
Previous: Summary of MI levels
Gal Chechik
2006-07-19
![\begin{displaymath}
\left[{I(X_1;S) + I(X_2;S)}\right] - I(X_1,X_2 ; S) \; .
\end{displaymath}](img22.png)
![\begin{displaymath}
\left[{I(X_1;S) + I(X_2;S)}\right] - I(X_1,X_2 ; S) \; .
\end{displaymath}](img22.png)
![\begin{displaymath}
SR = \left[{I(X_1;S) + I(X_2;S)}\right] - I(X_1,X_2 ; S)
= I(X_1;X_2) - I(X_1;X_2\vert S) \;,
\end{displaymath}](img23.png)

![]() stimuli, estimating redundancy in three neurons with dynamical range
of
stimuli, estimating redundancy in three neurons with dynamical range
of ![]() values requires at least
values requires at least ![]() stimulus repeats, which are
extremely hard to obtain in electrophysiological experiments. With the
conditional independence approximation, the number of parameters that
are required to compute the MI depends linearly, rather than
exponentially, on the number of neurons, making MI estimation
manageable. Furthermore, using the conditional-independence
approximation allowed us to increase our sample using neuronal pairs
and triplets that were not recorded simultaneously. Finally, such
conditional independence approximations are prominent in learning
multivariate distributions and often allow more reliable estimation
with limited samples [2]. The lesson learned from this
field is that when distributions are estimated from examples, better
accuracies are often obtained when applying �incorrect� independence
approximations, since these allow more reliable estimation of the
joint distribution. In fact, the conditional independence
approximation has been used previously in neural redundancy
calculations, for precisely the above reasons, for example by
[5].
stimulus repeats, which are
extremely hard to obtain in electrophysiological experiments. With the
conditional independence approximation, the number of parameters that
are required to compute the MI depends linearly, rather than
exponentially, on the number of neurons, making MI estimation
manageable. Furthermore, using the conditional-independence
approximation allowed us to increase our sample using neuronal pairs
and triplets that were not recorded simultaneously. Finally, such
conditional independence approximations are prominent in learning
multivariate distributions and often allow more reliable estimation
with limited samples [2]. The lesson learned from this
field is that when distributions are estimated from examples, better
accuracies are often obtained when applying �incorrect� independence
approximations, since these allow more reliable estimation of the
joint distribution. In fact, the conditional independence
approximation has been used previously in neural redundancy
calculations, for precisely the above reasons, for example by
[5].