Early Vision Using Distributions

or

Edge, Corner, and Junction Detection with the Generalized Compass Operator

Mark A. Ruzon

Download the Code

Voted "Best Research Web Page" in a Laboratory-Wide Poll

The goal of this research is the accurate detection, description, and linking of edges, corners, and junctions in natural images. It has been known for a long time that edges contain most of the information in an image while being represented far more compactly than the image itself. For this reason edge detection is perhaps the most basic (and therefore most studied) problem in computer vision. It is theorized to be the first step in image segmentation, the partitioning of an image into meaningful regions which, presumably, can then be analyzed independently to recognize different parts of a scene, and hopefully the context of the scene as a whole.

Corners and junctions (multiple corners in the same location) contain more information than edges because they occur less frequently. Edges without corners do not necessarily give humans enough cues to recognize even basic shapes, while corners without edges linking them can, surprisingly, allow rather complex recognition tasks to be performed. Corners and junctions can also be detected early in a visual system and used to help link edges together and determine the shape of an object.

One novel aspect of this research is that we do not smooth images in the usual sense. Smoothing is a popular way of removing noise or introducing scale into an image, but doing so removes edge and corner information as well. We generalize smoothing to vector quantization, which gives a more detailed description of part of an image.

This research advances the state of the art in edge and corner detection in three ways:

1. Most edge and corner models assume that the edge or corner divides an image window into two constant (at best, planar) regions; we allow arbitrary distributions of pixel values.
2. Because we do not model an image as a surface, we can use our framework on any image type (binary, greyscale, color, multi-spectral). One important consequence is that the treatment of color here is more intuitive than other models.
3. The detection of edges and the detection of corners need not be separate problems; they can be treated in a unified framework.

Skip ahead to the results.

Where do Other Edge Detection Algorithms Fail?

We now present two examples from natural images that typify situations where other edge detectors tend to miss edges:

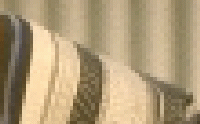In the image on the left, the helmet of a statue occludes the shadow of a windowsill behind it, creating a subjective boundary between the two regions because pixels in the shadow and the helmet are close in color. Since most edge detectors compute a weighted average of the pixels on each side, and since the two values representing the average color of the shadow and the helmet are close (assume our window is only the center part of the image), no edge is found. If we make our window bigger (bigger than our image, even), so that bright pixels from the bricks and the window are added, we can find the edge of the helmet, but we lose the edges between the window, the shadow, and the bricks. This is hardly the best we could hope for.

The image on the right also shares this phenomenon, but the difficulty is compounded by the fact that the two regions each have strong edges -- stronger, in a sense, than the boundary between them. The colors on each side are different, but their means are close together. The result is that edges will be found only between the stripes of each region, and the edges will likely connect across the desired boundary.

Read more about color edge detection.

The Compass Operator

Like most edge detectors (including Canny's), the compass operator divides an image window in half and compares the two sides to see if they are "different." But whereas most edge detectors compute an average value for each side and then compute the Euclidean distance, the compass operator allows multiple values to exist on each side. We take the colors in the window and quantize them to a variable number of values (if we restricted the number of values to 1 on each side, it would be equivalent to other operators), each with a weight depending on how many pixels have that color. Our representation is a signature, a set of point masses in color space.

Of course, we can no longer use the Euclidean distance to compute the distance between two signatures. Instead, we use the Earth Mover's Distance (EMD), which answers the following question: what is the minimum amount of physical "work" required to move the point masses in one signature so that they are in correspondence with the other? This is an instance of a very old problem called the transportation problem.

The idea of a "compass" comes from the fact that our window is circular, and the "needle," which divides the compass in half, spins until it finds the orientation that maximizes the EMD in the window. This maximum value is the strength of the edge, and we can combine it with the orientation (after rotating 90 degrees) to form a quantity similar to a gradient. From there, we can use standard techniques (non-maximal suppression, hysteresis thresholding) to extract edges.

Find out more about the compass operator's implementation.

Corners and Junctions: The Generalized Compass Operator

Almost all edge detectors (including the basic compass operator) rely on the assumption that the total amount of mass on each side is equal. Since models of corners violate this assumption, it is difficult, if not impossible, to extend these edge detectors to corners.

The underlying problem, however, is the same: given two adjacent regions, determine whether or not they are "different enough" from each other to declare the presence of an edge. The shape of the boundary between them is irrelevant. Thus, the generalized compass operator has an extra parameter indicating the angle subtended by the hypothesized corner. The two sides no longer have the same shape or the same total mass, but the EMD handles such partial matches easily; we simply find the minimum work needed to move the point masses of the smaller signature until they are in correspondence with a subset of the larger.

Skip ahead to the corner detection results.

Edge Detection Results

We compare the basic compass operator to the edge detector proposed by Canny (1986) that uses the multi-dimensional gradient proposed by Di Zenzo (1986). For both algorithms, we compute the magnitude and direction of the gradient (strength and orientation for the compass operator) followed by non-maximal suppression to extract the edges.

Our first example is the image with the subjective boundary. Dark values for the gradient magnitude, strength, and abnormality images are high. We show only the relevant edges extracted from each image.

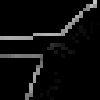			Canny gradient magnitude and edges, sigma = 1
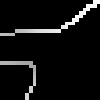			Canny gradient magnitude and edges, sigma = 4
			Canny gradient magnitude and edges, sigma = 16
			Compass Operator strength and edges, r = 8 (sigma = 4)

At small scales, there is not enough of a gradient to find the boundary of the helmet using Canny. We can recover it, but only by smoothing by a large amount so that the shadow behind the helmet is obliterated. The compass operator detects both. The size of the compass operator and the variance of the Gaussian used in this example is the same as that used in the second row.

Our other edge detection example shows the compass operator's superiority when interfering edges are present:

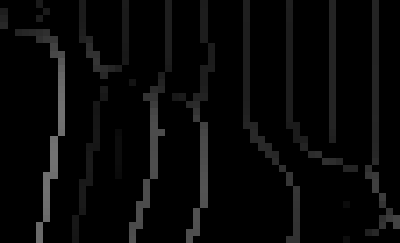		Canny gradient magnitude and edges, sigma = 1
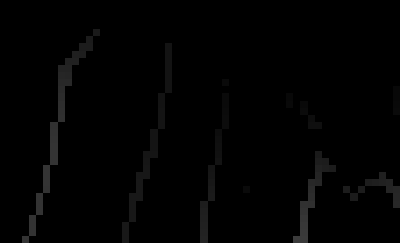		Canny gradient magnitude and edges, sigma = 8
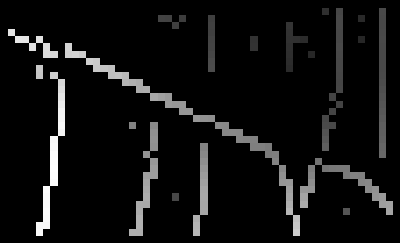		Compass Operator strength and edges, r = 16 (sigma = 8)

The Canny edge detector is unable to find the boundary, opting instead for the stripes in each region, while the compass operator finds most of the boundary.

Find out more about the relationship between the compass operator and Canny's operator.

Corner and Junction Detection Results

Corner and junction detection present additional complexity. Since they are point features, we must perform non-maximal suppression in all directions rather than one. Furthermore, we must estimate the angle subtended by a corner as well as its orientation. Therefore, our goal is to find local maxima in both location and angle. This will allow junctions to be detected, even though the corners which make up the junction may have the same location. In addition, we should be able to detect multiple corners having the same angle and location but different orientations.

We present results on two similar images, one containing only a corner, the other containing a junction. The length of the arrow is equal the radius of the operator.

The results are very promising. The two fabrics in the left image have very different textures with lots of color (and intensity) variation, including partial shadowing, yet the corner is correctly found. The slight discrepancy in the orientation of the "counterclockwise" side of the corner is due to the use of 15 degree sampling in orientation. In the right image, we find all three corners of the junction, but they do not exist at the same point. This happens because the three boundaries are not all straight. If necessary, the three corners could be labeled as a junction since their locations and orientations match favorably.

Most corner detectors published in the literature assume that each wedge is constant. Little work has been done in extending them to color images (though in many cases, this would not be too difficult), and no work that we are aware of handles regions with different textures such as those shown here.

Conclusions and Future Work

Vector quantization can be viewed as a generalization of smoothing where we allow for a more complex representation of the data (color signatures) than the weighted mean. The Earth Mover's Distance gives us an intuitive and efficient way to compute the distance between two signatures. The results show that edges can be detected in difficult situations involving subjective boundaries and interfering edges that violate the assumptions of Canny's edge detector.

A major advantage of using the EMD to compute distance is that it can handle partial matches, allowing corner detection to be done in the same framework as edge detection. Corners are defined to be relative maxima of the function defined over (x, y, theta).

While the description of edges, corners, and junctions is mostly complete, there is still much work to be done in the detection and linking of these features. Initial segmentation results from a "painting" algorithm, in which edges and corners with high responses are drawn onto the image and OR'ed together to form boundary regions, appear to be leading in the right direction.

A final aspect which deserves attention is the integration of information from multiple scales. There are two leading theories: the theory that says that for every point in an image there is one scale (or at least a finite range of scales) at which the "right" features can be detected. The other theory is that information from all scales should be compared in order to decide upon the proper interpretation of a pixel.

References

M. Ruzon and C. Tomasi, "Color Edge Detection with the Compass Operator," In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Ft. Collins, CO, V. 2, pp. 160-166, June 1999. [PS] [PDF]

M. Ruzon and C. Tomasi, "Corner Detection in Textured Color Images," In 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, V. 2, pp. 1039-1045, September 1999. [PS] [PDF]

M. Ruzon and C. Tomasi, "Edge, Junction, and Corner Detection Using Color Distributions," In IEEE Transactions on Pattern Analysis and Machine Intelligence, V. 23, No. 11, pp. 1281-1295, November 2001. [PDF]