Countless studies have found that “bias” – typically with respect to race and gender – pervades the embeddings and predictions of the black-box models that dominate natural language processing (NLP). For example, the language model GPT-3, of OpenAI fame, can generate racist rants when given the right prompt. Attempts to detect hate speech can itself harm minority populations, whose dialect is more likely to be flagged as hateful.
This, in turn, has led to a wave of work on how to “debias” models, only for others to find ways in which debiased models are still biased, and so on.
But are these claims of NLP models being biased (or unbiased) being made with enough evidence?
Consider the sentence “The doctor gave instructions to the nurse before she left.” A co-reference resolution system, tasked with finding which person the pronoun “she” is referring to1, may incorrectly predict that it’s the nurse. Does this incorrect prediction – which conforms to gender stereotypes that doctors are usually male – mean that the system is gender-biased? Possibly – but it may also make mistakes in the other direction with equal frequency (e.g., thinking “he” refers to a nurse when it doesn’t). What if the system makes gender-stereotypical mistakes on not one sentence, but 100, or 1000? Then we could be more confident in claiming that it’s biased.
In my ACL 2020 paper, “Measuring Fairness under Uncertainty with Bernstein Bounds”, I go over how, in the haste to claim the presence or absence of bias, the inherent uncertainty in measuring bias is often overlooked in the literature:
-
Bias is not a single number. When we test how biased a model is, we are estimating its bias on a sample of the data; our estimate may suggest that the model is biased or unbiased, but the opposite could still be true.
-
This uncertainty can be captured using confidence intervals. Instead of reporting a single number for bias, practitioners should report an interval, based on factors such as the desired confidence and the proposed definition of “bias”.
-
Existing datasets are too small to conclusively identify bias. Existing datasets for measuring specific biases can only be used to make 95% confidence claims when the bias estimate is egregiously high; to catch more subtle bias, the NLP community needs bigger datasets.
Although this problem can exist with any kind of model, we focus on a remedy for classification models in particular.
Bernstein-Bounded Unfairness
A bias estimate, made using a small sample of data, likely differs from the true bias (i.e., at the population-level). How can we express our uncertainty about the estimate? We propose a method called Bernstein-bounded unfairness that translates this uncertainty into a confidence interval2.
Let’s say we want to measure whether some protected group \(A\) – that is legally protected due to an attribute such as race or gender – is being discriminated against by some classifier, relative to some unprotected group \(B\). They occur in the population with frequency \(\gamma_A, \gamma_B\) respectively. We need
-
An annotation function \(f\) that maps each example \(x\) to \(A, B,\) or neither. Note that the annotation function maps inputs to the protected/unprotected groups, not to the output space \(Y\). For example, if we wanted to study how a sentiment classifier performed across different racial groups, then the inputs \(x\) would be sentences, labels \(y\) would be the sentiment, and the annotation function \(f\) might map \(x\) to {white, non-white} depending on the racial group of the sentence author.
-
A cost function \(c : (y, \hat{y}) \to [0,C]\) that describes the cost of incorrectly predicting \(\hat{y}\) when the true label is \(y\), where \(C\) is the maximum possible cost. Since a model making an incorrect prediction for \(x\) is an undesirable outcome for the group that \(x\) belongs to, we frame this as a cost that must be borne by the group.
We want to choose these functions such that our bias metric of choice – which we call the groupwise disparity \(\delta(f,c)\) – can be expressed as the difference in expected cost borne by the protected and unprotected groups. Given a model that makes predictions \(\hat{y}_a\) for protected \(x_a \in A\) and \(\hat{y}_b\) for unprotected \(x_b \in B\), we want to express the bias as:
\[\delta(f,c) = \mathbb{E}_a[c(y_a, \hat{y}_a)] - \mathbb{E}_b[c(y_b, \hat{y}_b)]\]If the protected group is incurring higher costs in expectation, it is being biased against. For example, if we want to determine whether a classifier is more accurate on the unprotected group \(B\), then we would set the cost function to be the 1-0 loss (1 for an incorrect prediction, 0 for a correct one). If \(B\) has a lower cost on average then \(A\), then it would mean that the classifier is more accurate on \(B\).
For a desired confidence level \(\rho \in [0,1)\), a dataset of \(n\) examples, and the variance \(\sigma^2\) of the amortized groupwise disparity across examples, the confidence interval \(t\) would be
\[\begin{aligned} t &= \frac{B + \sqrt{B^2 - 8 n \sigma^2 \log \left[\frac{1}{2} (1 - \rho) \right]}}{2n} \\ \text{where } B &= -\frac{2 C}{3 \gamma} \log \left[ \frac{1}{2} (1 - \rho) \right], \gamma = \min(\gamma_A, \gamma_B) \end{aligned}\]If we set \(\rho = 0.95\), we could claim with 95% confidence that the true bias experienced by the protected group lies in the interval \([ \hat{\delta} - t, \hat{\delta} + t]\), where \(\hat{\delta}\) is our bias estimate.
Why We Need Bigger Datasets
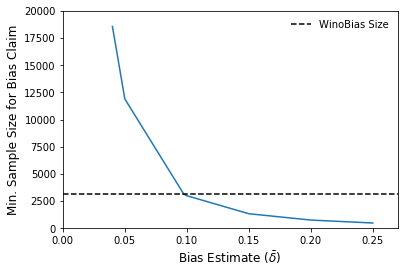
If we want to say with 95% confidence that a classifier is biased to some extent – but want to spend as little time annotating data as possible – we need to find the smallest \(n\) such that \(0 \not\in [ \hat{\delta} - t, \hat{\delta} + t]\). We can do this by working backwards from the formula for \(t\) given above (see paper for details).
Let’s go back to our original example. Say we want to figure out whether a co-reference resolution system, tasked with matching pronouns to the nouns they refer to, is gender-biased or not. We have a dataset of 500 examples to test whether the model does better on gender-stereotypical examples (e.g., a female nurse) than non-gender-stereotypical examples (e.g., a male nurse). Since we are measuring the difference in accuracy, we set the cost function to be the 1-0 loss.
On this dataset, our bias estimate for a model we’re evaluating is \(\bar{\delta} = 0.05\). Is this enough to claim with 95% confidence that the model is gender-biased?
In this scenario \(C = 1, \bar{\delta} = 0.05, \rho = 0.95\). We assume that there are equally many stereotypical and non-stereotypical examples and that the variance is maximal, so \(\gamma = 0.5, \sigma^2 = 4\).
With these settings, \(n > 11903\); we would need a dataset of more than 11903 examples to claim with 95% confidence that the co-reference resolution system is gender-biased. This is roughly 3.8 times larger than WinoBias, the largest dataset currently available for this purpose. We could only use WinoBias if \(\bar{\delta} = 0.0975\) – that is, if the sample bias were almost twice as high.
Conclusion
In the haste to claim the presence or absence of bias in models, the uncertainty in estimating bias is often overlooked in the literature. A model’s bias is often thought of as a single number, even though this number is ultimately an estimate and not the final word on whether the model is or is not biased.
We proposed a method called Bernstein-bounded unfairness for capturing this uncertainty using confidence intervals. To faithfully reflect the range of possible conclusions, we recommend that NLP practitioners measuring bias not only report their bias estimate but also this confidence interval.
What if we want to catch more subtle bias? Although it may be possible to derive tighter confidence intervals, what we really need are larger bias-specific datasets. The datasets we currently have are undoubtedly helpful, but they need to be much larger in order to diagnose biases with confidence.
Acknowledgements
Many thanks to Krishnapriya Vishnubhotla, Michelle Lee, and Kaitlyn Zhou for their feedback on this blog post.
-
The goal of coreference resolution more broadly is to find all expressions that refer to the same entity in a text. For example, in “I gave my mother Sally a gift for her birthday.”, the terms “my mother”, “Sally”, and “her” all refer to the same entity. ↩
-
We use Bernstein’s inequality to derive the confidence intervals, hence the name Bernstein-bounded unfairness. This inequality tells us with what probability the average of \(n\) independent random variables will be within a constant $t$ of their true mean $\mu$. ↩