Data augmentation is a de facto technique used in nearly every state-of-the-art machine learning model in applications such as image and text classification. Heuristic data augmentation schemes are often tuned manually by human experts with extensive domain knowledge, and may result in suboptimal augmentation policies. In this blog post, we provide a broad overview of recent efforts in this exciting research area, which resulted in new algorithms for automating the search process of transformation functions, new theoretical insights that improve the understanding of various augmentation techniques commonly used in practice, and a new framework for exploiting data augmentation to patch a flawed model and improve performance on crucial subpopulation of data.
Why Data Augmentation?
Modern machine learning models, such as deep neural networks, may have billions of parameters and require massive labeled training datasets—which are often not available. The technique of artificially expanding labeled training datasets—known as data augmentation—has quickly become critical for combating this data scarcity problem. Today, data augmentation is used as a secret sauce in nearly every state-of-the-art model for image classification, and is becoming increasingly common in other modalities such as natural language understanding as well. The goal of this blog post is to provide an overview of recent efforts in this exciting research area.
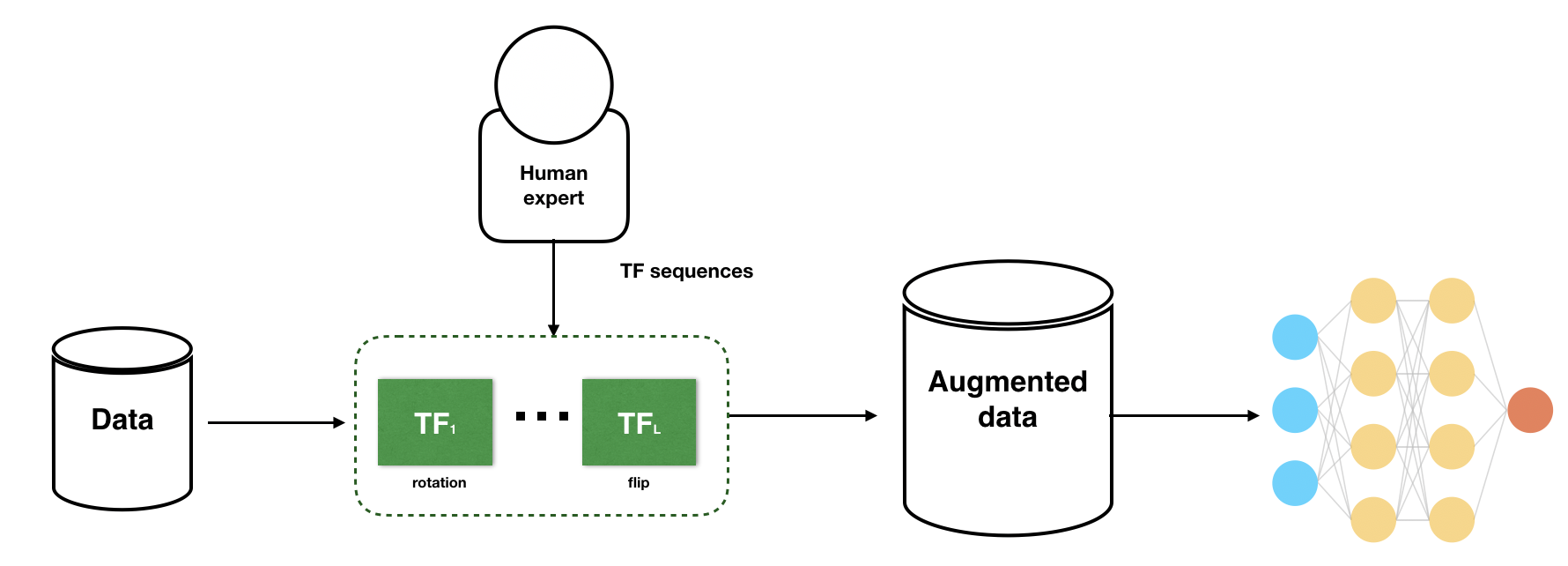
Heuristic data augmentation schemes often rely on the composition of a set of simple transformation functions (TFs) such as rotations and flips (see Figure 1). When chosen carefully, data augmentation schemes tuned by human experts can improve model performance. However, such heuristic strategies in practice can cause large variances in end model performance, and may not produce augmentations needed for state-of-the-art models.
The Open Challenges in Data Augmentation
The limitations of conventional data augmentation approaches reveal huge opportunities for research advances. Below we summarize a few challenges that motivate some of the works in the area of data augmentation.
-
From manual to automated search algorithms: As opposed to performing suboptimal manual search, how can we design learnable algorithms to find augmentation strategies that can outperform human-designed heuristics?
-
From practical to theoretical understanding: Despite the rapid progress of creating various augmentation approaches pragmatically, understanding their benefits remains a mystery because of a lack of analytic tools. How can we theoretically understand various data augmentations used in practice?
-
From coarse-grained to fine-grained model quality assurance: While most existing data augmentation approaches focus on improving the overall performance of a model, it is often imperative to have a finer-grained perspective on critical subpopulations of data. When a model exhibits inconsistent predictions on important subgroups of data, how can we exploit data augmentations to mitigate the performance gap in a prescribed way?
In this blog, we will describe ideas and recent research works leading the way to overcome these challenges above.
Practical Methods of Learnable Data Augmentations
Learnable data augmentation is promising, in that it allows us to search for more powerful parameterizations and compositions of transformations. Perhaps the biggest difficulty with automating data augmentation is how to search over the space of transformations. This can be prohibitive due to the large number of transformation functions and associated parameters in the search space. How can we design learnable algorithms that explore the space of transformation functions efficiently and effectively, and find augmentation strategies that can outperform human-designed heuristics? In response to the challenge, we highlight a few recent methods below.
TANDA: Transformation Adversarial Networks for Data Augmentations
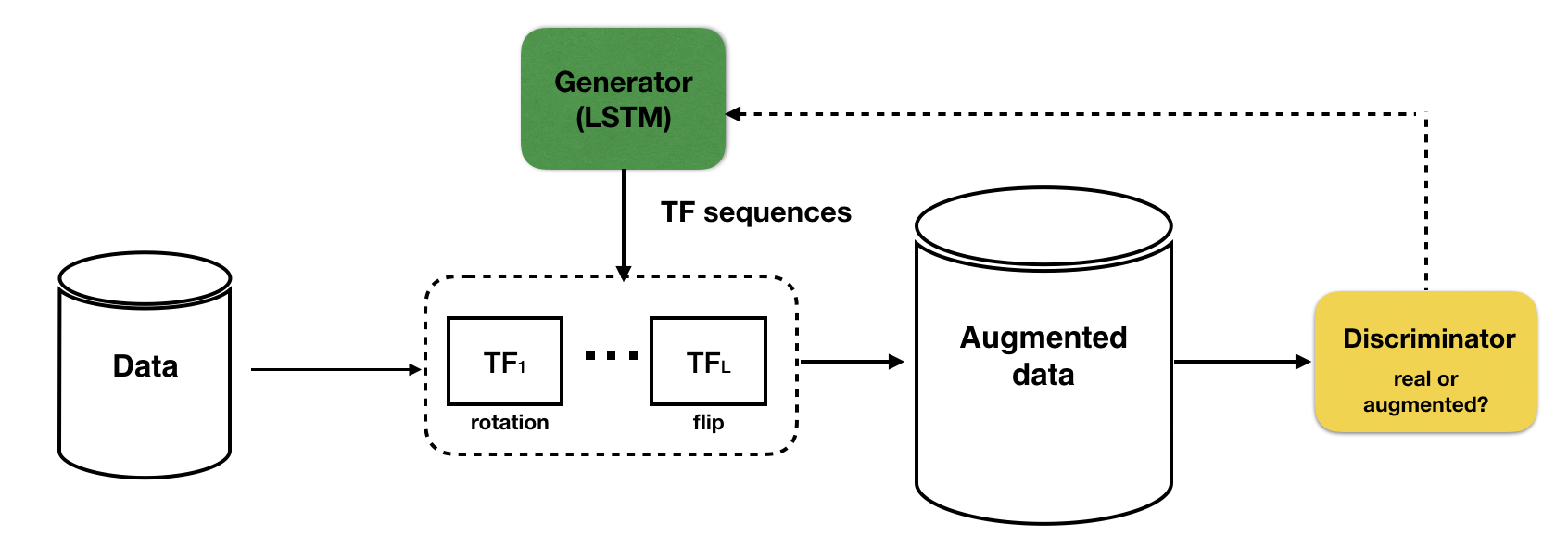
To address this problem, TANDA (Ratner et al. 2017) proposes a framework to learn augmentations, which models data augmentations as sequences of Transformation Functions (TFs) provided by users. For example, these might include “rotate 5 degrees” or “shift by 2 pixels”. At the core, this framework consists of two components (1) learning a TF sequence generator that results in useful augmented data points, and (2) using the sequence generator to augment training sets for a downstream model. In particular, the TF sequence generator is trained to produce realistic images by having to fool a discriminator network, following the GANs framework (Goodfellow et al. 2014). The underlying assumption here is that the transformations would either lead to realistic images, or indistinguishable garbage images that are off the manifold. As shown in Figure 1, the objective for the generator is to produce sequences of TFs such that the augmented data point can fool the discriminator; whereas the objective for the discriminator is to produce values close to 1 for data points in the original training set and values close to 0 for augmented data points.
AutoAugment and Further Improvement Using a similar framework, AutoAugment (Cubuk et al. 2018) developed by Google demonstrated state-of-the-art performance using learned augmentation policies. In this work, a TF sequence generator learns to directly optimize for validation accuracy on the end model. Several subsequent works including RandAugment (Cubuk et al. 2019) and Adversarial AutoAugment (Zhang et al. 2019) have been proposed to reduce the computational cost of AutoAugment, establishing new state-of-the-art performance on image classification benchmarks.
Theoretical Understanding of Data Augmentations
Despite the rapid progress of practical data augmentation techniques, precisely understanding their benefits remains a mystery. Even for simpler models, it is not well-understood how training on augmented data affects the learning process, the parameters, and the decision surface. This is exacerbated by the fact that data augmentation is performed in diverse ways in modern machine learning pipelines, for different tasks and domains, thus precluding a general model of transformation. How can we theoretically characterize and understand the effect of various data augmentations used in practice? To address this challenge, our lab has studied data augmentation from a kernel perspective, as well as under a simplified linear setting.
Data Augmentation As a Kernel
Dao et al. 2019 developed a theoretical framework by modeling data augmentation as a Markov Chain, in which augmentation is performed via a random sequence of transformations, akin to how data augmentation is performed in practice. We show that the effect of applying the Markov Chain on the training dataset (combined with a k-nearest neighbor classifier) is akin to using a kernel classifier, where the kernel is a function of the base transformations.
Built on the connection between kernel theory and data augmentation, Dao et al. 2019 show that a kernel classifier on augmented data approximately decomposes into two components: (i) an averaged version of the transformed features, and (ii) a data-dependent variance regularization term. This suggests a more nuanced explanation of data augmentation—namely, that it improves generalization both by inducing invariance and by reducing model complexity. Dao et al. 2019 validate the quality of our approximation empirically, and draw connections to other generalization-improving techniques, including recent work on invariant learning (van der Wilk et al. 2018) and robust optimization (Namkoong & Duchi, 2017).
Data Augmentation Under A Simplified Linear Setting
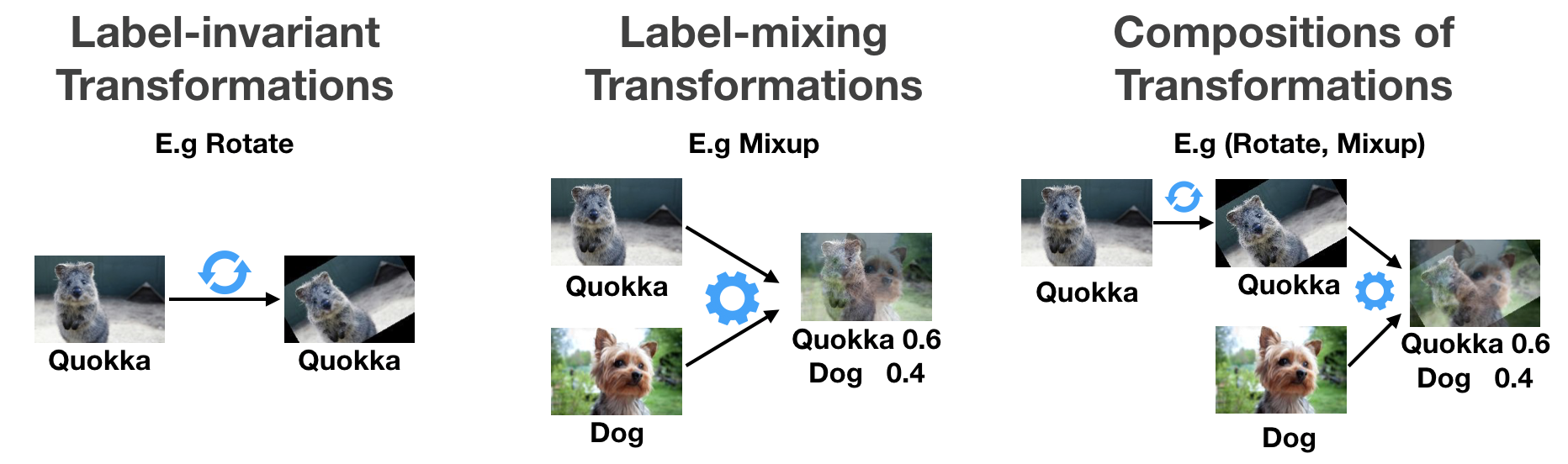
One limitation of the above works is that it is challenging to pin down the effect of applying a particular transformation on the resulting kernel. Furthermore, it is not yet clear how to apply data augmentation efficiently on kernel methods to get comparable performance to neural nets. In more recent work, we consider a simpler linear setting that is capable of modeling a wide range of linear transformations commonly used in image augmentation, as shown in Figure 3.
Theoretical Insights. We offer several theoretical insights by considering an over-parametrized linear model, where the training data lies in a low-dimensional subspace. We show that label-invariant transformations can add new information to the training data, and estimation error of the ridge estimator can be reduced by adding new points that are outside the span of the training data. In addition, we show that mixup (Zhang et al., 2017 can play an effect of regularization through shrinking the weight of the training data relative to the L2 regularization term on the training data.
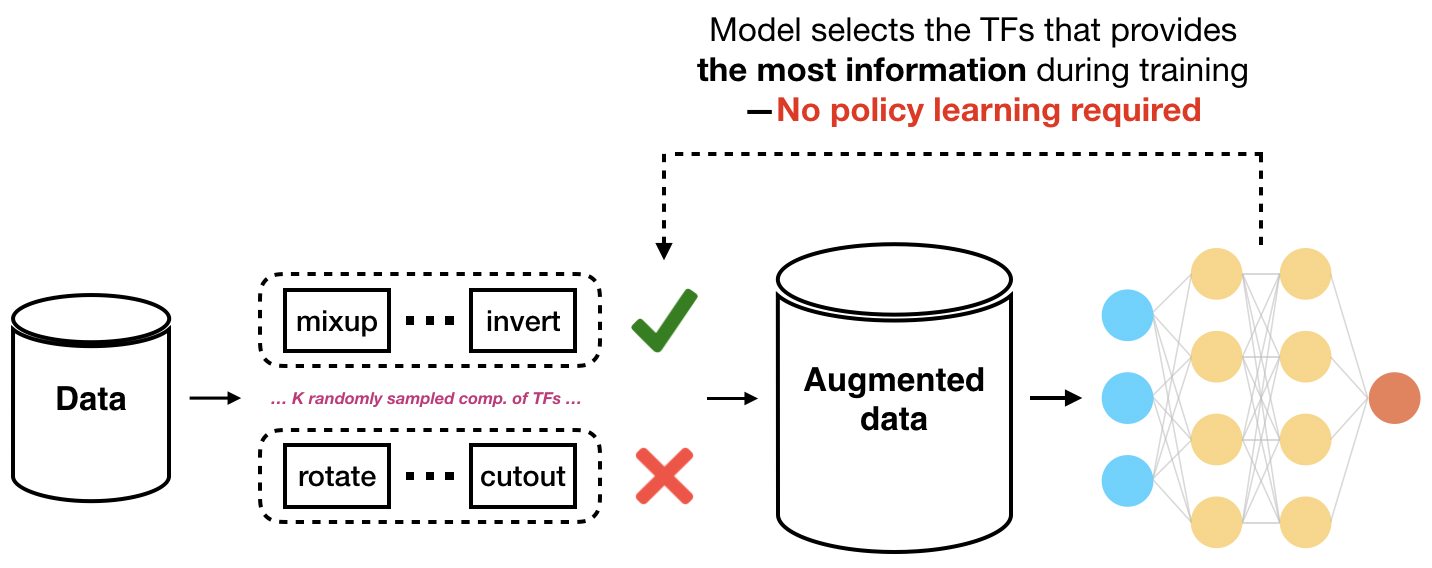
Theory-inspired New State-of-the-art. One insight from our theoretical investigation is that different (compositions of) transformations show very different end performance. Inspired by this observation, we’d like to make use of the fact that certain transformations are better performing than others. We propose an uncertainty-based random sampling scheme which, among the transformed data points, picks those with the highest losses, i.e. those “providing the most information” (see Figure 4). Our sampling scheme achieves higher accuracy by finding more useful transformations compared to RandAugment on three different CNN architectures, establishing new state-of-the-art performance on common benchmarks. For example, our method outperforms RandAugment by 0.59% on CIFAR-10 and 1.24% on CIFAR-100 using Wide-ResNet-28-10. Please check out our full paper here. Our code will be released soon for you to try out!
New Direction: Data Augmentations for Model Patching
Most machine learning research carried out today is still solving fixed tasks. However, in the real world, machine learning models in deployment can fail due to unanticipated changes in data distribution. This raises the concerning question of how we can move from model building to model maintenance in an adaptive manner. In our latest work, we propose model patching—the first framework that exploits data augmentation to mitigate the performance issues of a flawed model in deployment.
A Medical Use Case of Model Patching
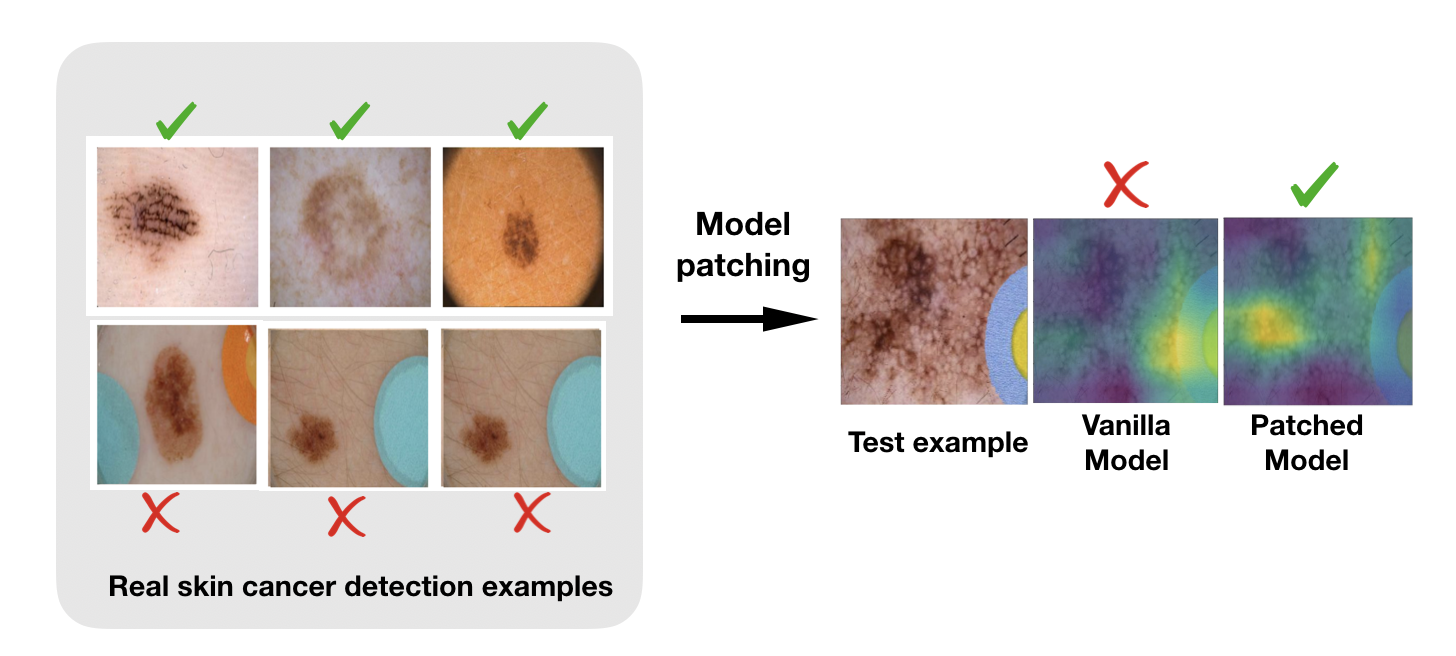
To provide a concrete example, in skin cancer detection, researchers have shown that standard classifiers have drastically different performance on two subgroups of the cancerous class, due to the classifier’s association between colorful bandages with benign images (see Figure 5, left). This subgroup performance gap has also been studied in parallel research from our group (Oakden-Rayner et al., 2019), and arises due to classifier’s reliance on subgroup-specific features, e.g. colorful bandages.
In order to fix such flaws in a deployed model, domain experts have to resort to manual data cleaning to erase the differences between subgroups, e.g. removing markings on skin cancer data with Photoshop (Winkler et al. 2019), and retrain the model with the modified data. This can be extremely laborious! Can we somehow learn transformations that allow augmenting examples to balance population among groups in a prescribed way? This is exactly what we are addressing through this new framework of model patching.
CLAMP: Class-conditional Learned Augmentations for Model Patching
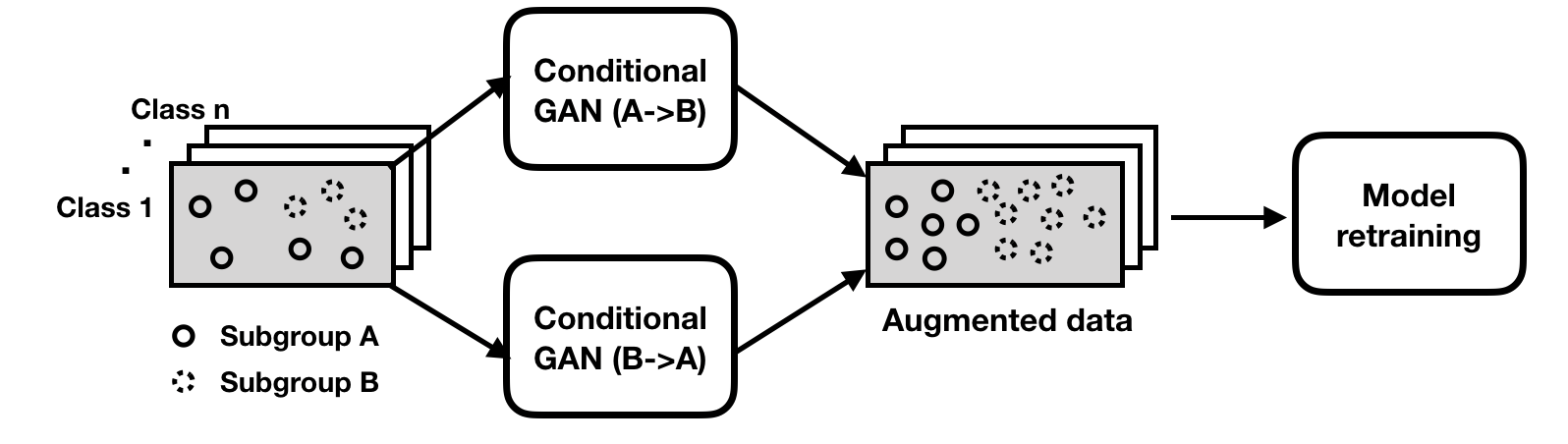
The conceptual framework of model patching consists of two stages (as shown in Figure 6).
- Learn inter-subgroup transformations between different subgroups. These transformations are class-preserving maps that allow semantically changing a datapoint’s subgroup identity (e.g. add or remove colorful bandages).
- Retrain to patch the model with augmented data, encouraging the classifier to be robust to their variations.
We propose CLAMP, an instantiation of our first end-to-end model patching framework. We combine a novel consistency regularizer with a robust training objective that is inspired by recent work of Group Distributionally Robust Optimization (GDRO, Sagawa et al. 2019). We extend GDRO to a class-conditional training objective that jointly optimizes for the worst-subgroup performance in each class. CLAMP is able to balance the performance of subgroups within each class, reducing the performance gap by up to 24x. On a skin cancer detection dataset ISIC, CLAMP improves robust accuracy by 11.7% compared to the robust training baseline. Through visualization, we also show in Figure 5 that CLAMP successfully removes the model’s reliance on the spurious feature (colorful bandages), shifting its attention to the skin lesion—true feature of interest.
Our results suggest that the model patching framework is a promising direction for automating the process of model maintenance. In fact, model patching is becoming a late breaking area that would alleviate the major problem in safety-critical systems, including healthcare (e.g. improving models to produce MRI scans free of artifact) and autonomous driving (e.g. improving perception models that may have poor performance on irregular objects or road conditions). We envision that model patching can be widely useful for many other domain applications. If you are intrigued by the latest research on model patching, please follow our Hazy Research repository on Github where the code will be released soon. If you have any feedback for our drafts and latest work, we’d like to hear from you!
Further Reading
- Automating the Art of Data Augmentation (Part I: Overview)
- Automating the Art of Data Augmentation (Part II: Practical Methods)
- Automating the Art of Data Augmentation (Part III: Theory)
- Automating the Art of Data Augmentation (Part IV: New Direction)
Acknowledgments
Thanks to members of Hazy Research who provided feedback on the blog post. Special thanks to Sidd Karamcheti and Andrey Kurenkov from the SAIL blog team for the editorial help.
About the Author
Sharon Y. Li is a postdoctoral fellow at Stanford, working with Chris Ré. She is an incoming Assistant Professor in the department of Computer Sciences at University of Wisconsin-Madison. Her research focuses on developing machine learning models and systems that can reduce human supervision during training, and enhance reliability during deployment in the wild.