Nobody likes chores — can we build robots to do these chores, such as cooking, for us? A common paradigm for training agents to perform various tasks is to train a separate agent on each task, completely from scratch, with reinforcement learning. However, training a robot to cook with reinforcement learning from scratch in each person’s home would completely fail, as it would result in many disasters (e.g., kitchen fires), would require a lot of supervision from each person to reward the robot for successfully cooking meals, and would take a long time (learning even simple tasks from scratch can take reinforcement learning agents millions of attempts).
Instead, it would be ideal if we could train a robot to be able to quickly adapt to various home kitchens, after first training in many kitchens in a robot chef factory. Intuitively, this should be possible since different tasks and environments share considerable structure (e.g., cooking pizza in one kitchen is similar to cooking a hamburger in another kitchen), which can make learning each task easier and more efficient.
Fortunately, meta-reinforcement learning seeks this exact goal of training agents to adapt to new tasks from very few interactions on the new task, after first training on many similar tasks. So, why aren’t robots cooking in our kitchens today? To answer this question, we’ll turn our attention to the problem of meta-exploration: how to best spend these few interactions exploring the new task. For example, in order to adapt to a new kitchen, a robot chef should ideally spend its few interactions exploring the new kitchen to find the ingredients, which will allow it to later cook a meal (solve the task). In this blog post, we’ll cover and solve two key challenges about meta-exploration that keep humans in the kitchen.
-
First, we’ll show that existing meta-reinforcement learning approaches suffer from a chicken-and-egg coupling problem: learning to explore and find the ingredients only helps a robot prepare a meal if it already knows how to cook, but the robot can only learn to cook if it already knows where the ingredients are. We’ll avoid this cyclic dependence of learning to explore and learning to execute (solve the task) by proposing an objective to learn them independently of each other.
-
Second, we’ll observe that the standard meta-reinforcement learning problem setting expects robots to cook the correct meal by trial-and-error, without even being told what meal to cook, which unnecessarily complicates the meta-exploration problem. To avoid this, we propose instruction-based meta-reinforcement learning, where the robot receives instructions specifying what meal to cook.
Standard Meta-Reinforcement Learning
Before we dive in, let’s review the standard meta-reinforcement learning (meta-RL) problem statement. In meta-reinforcement learning, an agent (e.g., a robot chef) trains on many tasks (different recipes) and environments (different kitchens), and then must accomplish a new task in a new environment during meta-testing. When presented with a new task and environment, the agent is allowed to first spend an episode exploring, gathering any necessary information (e.g., locating the ingredients), before execution episodes, where the agent must accomplish the task (e.g., cook a meal).
In more formal language, standard meta-RL considers a family of problems, where each problem \(\mu\) identifies a reward function \(\mathcal{R}_\mu\) (e.g., cook a pizza) and transition dynamics (e.g., a kitchen). Using the terminology from Duan et al., 2016, we define a trial to consist of several episodes in the same problem. The first episode is the exploration episode, where the agent is allowed to gather information, without needing to maximize returns. All subsequent episodes are execution episodes, where the agent must accomplish the task. The goal is to maximize the returns achieved during the execution episodes of meta-testing trials, after first training on many trials during meta-training.
Decoupled Reward-free Exploration and Execution in Meta-Reinforcement Learning (DREAM)
A chicken-and-egg coupling problem. A common approach (Wang et al., 2016, Duan et al., 2016) for the meta-exploration problem is to optimize a recurrent policy that performs both exploration and execution episodes end-to-end based on the execution episode rewards. The hope is to capture the information learned during the exploration episode in the recurrent policy’s hidden state, which will then be useful for execution episodes. However, this leads to a chicken-and-egg coupling problem, where learning good exploration behaviors requires already having learned good execution behaviors and vice-versa, which prevents such an approach from learning.
For example, if a robot chef fails to discover the locations of ingredients in a kitchen (bad exploration), then it cannot possibly learn how to cook (bad execution). On the other hand, if the robot does not know how to cook (bad execution), then no matter what it does during the exploration episode, it will still not successfully cook a meal, making learning exploration challenging. Since robots can’t cook or explore at the beginning of training, they get stuck in this local optimum and have a hard time learning either.

Avoiding the coupling problem with DREAM. To avoid the chicken-and-egg coupling problem, we propose a method to break the cyclic dependency between learning exploration and learning execution behaviors, which we call DREAM. Intuitively, good exploration can be learned by trying to recover the information necessary for executing instructions. Therefore, from a high-level, DREAM consists of two main steps: 1) simultaneously learn an execution policy independently from exploration and learn what information is necessary for execution and 2) learn an exploration policy to recover that information.
More concretely, in the first step, we train an execution policy \(\pi^\text{exec}\) conditioned on the problem identifier \(\mu\), which in the cooking example, may either directly identify attributes of the kitchen (e.g., wall color or ingredient locations), or simply be a unique identifier (e.g., a one-hot) for each kitchen. This problem identifier (directly or indirectly) encodes all the information necessary to solve tasks in the kitchen, allowing the execution policy to learn independently from exploration, which avoids the coupling problem. At the same time, our goal in the first step is to identify only the information necessary for executing instructions, and the problem identifier may also encode extraneous information, such as the wall color. To remove this, we apply an information bottleneck to obtain a bottlenecked representation \(z\), which we use for training an exploration policy \(\pi^\text{exp}\).
In the second step, once we’ve obtained a bottleneck representation \(z\) that ideally contains only the information necessary for executing instructions, we can train an exploration policy \(\pi^\text{exp}\) to recover this information in the exploration episode. To do this, we roll-out the exploration policy to obtain an episode \(\tau\) and then reward the policy based on how well this episode encodes the information contained in \(z\). Roughly, this reward is the mutual information \(I(z; \tau)\) between the bottlenecked representation \(z\) and the episode \(\tau\).
The problem identifier \(\mu\) is easy to provide during meta-training by simply assigning each problem a unique one-hot, but is typically unavailable or unhelpful during meta-testing (e.g., if \(\mu\) is a completely new one-hot). This might seem concerning, since, during meta-training, the execution policy conditions on \(z\), which requires knowing \(\mu\). However, since the exploration policy is trained to produce exploration trajectories \(\tau\) that contain the same information as \(z\), we can directly swap \(\tau\) for \(z\) at meta-test time by rolling out the exploration policy. See our paper for the details!
Instruction-based Meta-Reinforcement Learning (IMRL)
Improving the standard meta-RL setting. A second meta-exploration challenge concerns the meta-reinforcement learning setting itself. While the above standard meta-RL setting is a useful problem formulation, we observe two areas that can be made more realistic. First, the standard setting requires the agent to infer the task (e.g., the meal to cook) from reward observations, which can be needlessly inefficient. In more realistic situations, the user would just tell the agent what they want, instead.
Second, while the standard meta-RL setting leverages shared structure between different problems (environment and task pairs), it does not capture shared structure between different tasks in the same environment. More concretely, the task is fixed across all episodes in a trial, and in order to perform a new task (e.g., cook a new meal), the agent requires another exploration episode, even when the underlying environment (e.g., the kitchen) stays the same. Instead, an agent would ideally be able to perform many tasks after a single exploration episode. For example, after exploring the kitchen to find any ingredients, an ideal robot chef would be able to then cook any meal involving those ingredients, whereas an agent trained in the standard meta-reinforcement learning setting would only be able to cook a single meal.
These two areas can obscure the meta-exploration problem of how to optimally spend the exploration episode, as the former requires unnecessary exploration to infer the task, while the latter only requires the agent to explore to discover information relevant to a single task. While intuitively, the agent should spend the exploration episode gathering useful information for later execution episodes, in many cases, optimal exploration collapses to simply solving the task. For example, the agent can only discover that the task is to cook pizza by successfully cooking pizza and receiving positive rewards, only to do the same thing again and again on future execution episodes. This can make the exploration episode nearly useless.
Instruction-based meta-RL (IMRL). To make the meta-RL setting more realistic, we propose a new setting called instruction-based meta-RL (IMRL), which addresses the two above areas by (i) providing the agent with instructions (e.g., "cook pizza" or a one-hot representation) that specify the task during execution episodes and (ii) varying the task by providing a different instruction on each execution episode. Then, for example, after meta-training in different kitchens at a factory, a robot chef could begin cooking many different meals specified by a human in a new home kitchen, after a single setup period (exploration episode).
Reward-free adaptation. In the standard meta-RL setting, the agent requires reward observations during exploration episodes in order to infer the task. However, by receiving instructions that specify the task in IMRL, a further benefit is that the agent no longer requires observing rewards to adapt to new tasks and environments. Concretely, IMRL enables reward-free adaptation, where during meta-training, the agent uses reward observations during execution episodes to learn to solve the task, but does not observe rewards during exploration episodes. During meta-testing, the agent never observes any rewards. This enables modeling real-world deployment situations where gathering reward supervision is really expensive. For example, a robot chef would ideally be able to adapt to a home kitchen without any supervision from a human.
Is IMRL general? Importantly, setting the instruction to always be some "empty" instruction recovers the standard meta-RL setting. In other words, standard meta-RL is just IMRL, where the user's desires are fixed within a trial and the user says nothing for the instructions. Therefore, algorithms developed for IMRL can also be directly applied to the standard setting and vice-versa.
Results


Sparse-reward 3D visual navigation. In one experiment from our paper, we evaluate DREAM on the sparse-reward 3D visual navigation problem family proposed by Kamienny et al., 2020 (pictured above), which we've made harder by including a visual sign and more objects. We use the IMRL setting with reward-free adaptation. During execution episodes, the agent receives an instruction to go to an object: a ball, block or key. The agent starts episodes on the far side of the barrier, and must walk around the barrier to read the sign (highlighted in yellow), which in the two versions of the problem, either specify going to the blue or red version of the object. The agent receives 80x60 RGB images as observations and can turn left or right, or move forward. Going to the correct object gives reward +1 and going to the wrong object gives reward -1.
DREAM learns near-optimal exploration and execution behaviors on this task, which are pictured below. On the left, DREAM spends the exploration episode walking around the barrier to read the sign, which says blue. On the right, during an execution episode, DREAM receives an instruction to go to the key. Since DREAM already read that the sign said blue during the exploration episode, it goes to the blue key.
Behaviors learned by DREAM


Comparisons. Broadly, prior meta-RL approaches fall into two main groups: (i) end-to-end approaches, where exploration and execution are optimized end-to-end based on execution rewards, and (ii) decoupled approaches, where exploration and execution are optimized with separate objectives. We compare DREAM with state-of-the-art approaches from both categories. In the end-to-end category, we compare with:
-
RL\(^2\)12, the canonical end-to-end approach, which learns a recurrent policy conditioned on the entire sequence of past state and reward observations.
-
VariBAD3, which additionally adds auxiliary loss functions to the hidden state of the recurrent policy to predict the rewards and dynamics of the current problem. This can be viewed as learning the belief state4, a sufficient summary of all of its past observations.
-
IMPORT5, which additionally leverages the problem identifier to help learn execution behaviors.
Additionally, in the decoupled category, we compare with:
- PEARL-UB, an upperbound on PEARL6. We analytically compute the expected rewards achieved by the optimal problem-specific policy that explores with Thompson sampling7 using the true posterior distribution over problems.
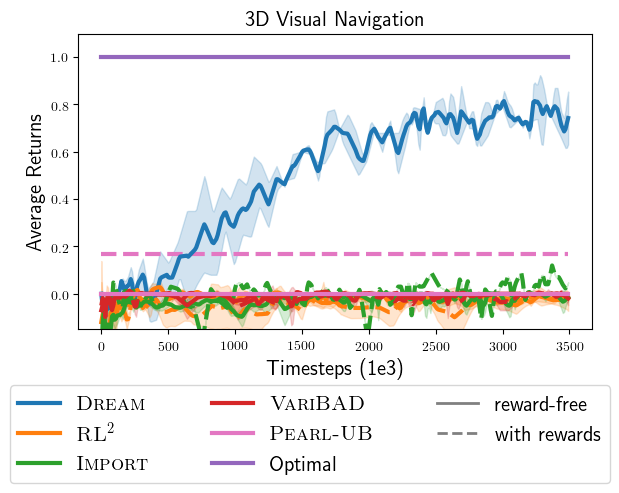
Quantitative results. Below, we plot the returns achieved by all approaches. In contrast to DREAM, which achieves near-optimal returns, we find that the end-to-end approaches never read the sign, and consequently avoid all objects, in fear of receiving negative reward for going to the wrong object. This happens even when they are allowed to observe rewards in the exploration episode (dotted lines). Therefore, they achieve no rewards, which is indicative of the coupling problem.
On the other hand, while existing approaches in the decoupled category avoid the coupling problem, optimizing their objectives does not lead to the optimal exploration policy. For example, Thompson sampling approaches (PEARL-UB) do not achieve optimal reward, even with the optimal problem-specific execution policy and access to the true posterior distribution over problems. To see this, recall that Thompson sampling explores by sampling a problem from the posterior distribution and following the execution policy for that problem. Since the optimal execution policy directly goes to the correct object, and never reads the sign, Thompson sampling never reads the sign during exploration. In contrast, a nice property of DREAM is that with enough data and expressive-enough policy classes, it theoretically learns optimal exploration and execution.
Additional results. In our paper, we also evaluate DREAM on additional didactic problems, designed to to answer the following questions:
-
Can DREAM efficiently explore to discover only the information required to execute instructions?
-
Can DREAM generalize to unseen instructions and environments?
-
Does DREAM also show improved results in the standard meta-RL setting, as well as instruction-based meta-RL?
Broadly, the answer is yes to all of these questions. Check out our paper for detailed results!
Conclusion
Summary. In this blog post, we tackled the problem of meta-exploration: how to best gather information in a new environment in order to perform a task. To do this, we examined and addressed two key challenges.
-
First, we saw how existing meta-RL approaches that optimize both exploration and execution end-to-end to maximize reward fall prey to a chicken-and-egg problem. If the agent hasn’t learned to explore yet, then it can’t gather key information (e.g., the location of ingredients) required for learning to solve tasks (e.g., cook a meal). On the other hand, if the agent hasn’t learned to solve tasks yet, then there’s no signal for learning to explore, as it’ll fail to solve the task no matter what. We avoided this problematic cycle by proposing a decoupled objective (DREAM), which learns to explore and learns to solve tasks independently from each other.
-
Second, we saw how the standard meta-RL setting captures the notion of adapting to a new environment and task, but requires the agent to unnecessarily explore to infer the task (e.g., what meal to cook) and doesn’t leverage the shared structure between different tasks in the same environment (e.g., cooking different meals in the same kitchen). We addressed this by proposing instruction-based meta-RL (IMRL), which provides the agent with an instruction that specifies the task and requires the agent to explore and gather information useful for many tasks.
DREAM and IMRL combine quite nicely: IMRL enables reward-free adaptation in principle, and DREAM achieves it in practice. Other state-of-the-art approaches we tested weren’t able to achieve reward-free adaptation, due to the chicken-and-egg coupling problem.
What’s next? There’s a lot of room for future work — here are a few directions to explore.
-
More sophisticated instruction and problem ID representations. This work examines the case where the instructions and problem IDs are represented as unique one-hots, as a proof of concept. Of course, in the real world, instructions and problem IDs might be better represented with natural language, or images (e.g., a picture of the meal to cook).
-
Applying DREAM to other meta-RL settings. DREAM applies generally to any meta-RL setting where some information is conveyed to the agent and the rest must be discovered via exploration. In this work, we studied two such instances — in IMRL, the instruction conveys the task and in the standard meta-RL setting, everything must be discovered via exploration — but there are other settings worth examining, too. For example, we might want to convey information about the environment to the agent, such as the locations of some ingredients, or that the left burner is broken, so the robot chef should use the right one.
-
Seamlessly integrating exploration and execution. In the most commonly studied meta-RL setting, the agent is allowed to first gather information via exploration (exploration episode) before then solving tasks (execution episodes). This is also the setting we study, and it can be pretty realistic. For example, a robot chef might require a setup phase, where it first explores a home kitchen, before it can start cooking meals. On the other hand, a few works, such as Zintgraf et al., 2019, require the agent to start solving tasks from the get-go: there are no exploration episodes and all episodes are execution episodes. DREAM can already operate in this setting, by just ignoring the rewards and exploring in the first execution episode, and trying to make up for the first execution episode with better performance in later execution episodes. This works surprisingly well, but it’d be nice to more elegantly integrate exploration and execution.
Acknowledgements
This is work done with my fantastic collaborators Aditi Raghunathan, Percy Liang, and Chelsea Finn. You can check out our full paper on ArXiv and our source code on GitHub. You can also find a short talk on this work here.
Many thanks to Andrey Kurenkov for comments and edits on this blog post!
The icons used in the above figures were made by Freepik, ThoseIcons, dDara, mynamepong, Icongeek26, photo3idea_studio and Vitaly Gorbachev from flaticon.com.
-
Y. Duan, J. Schulman, X. Chen, P. L. Bartlett, I. Sutskever, and P. Abbeel. RL2: Fast reinforcement learning via slow reinforcement learning. arXiv preprint arXiv:1611.02779, 2016. ↩
-
J. X. Wang, Z. Kurth-Nelson, D. Tirumala, H. Soyer, J. Z. Leibo, R. Munos, C. Blundell, D. Kumaran, and M. Botvinick. Learning to reinforcement learn. arXiv preprint arXiv:1611.05763, 2016. ↩
-
L. Zintgraf, K. Shiarlis, M. Igl, S. Schulze, Y. Gal, K. Hofmann, and S. Whiteson. VariBAD A very good method for bayes-adaptive deep RL via meta-learning. arXiv preprint arXiv:1910.08348, 2019. ↩
-
L. P. Kaelbling, M. L. Littman, and A. R. Cassandra. Planning and acting in partially observable stochastic domains. Artificial intelligence, 101(1):99–134, 1998. ↩
-
P. Kamienny, M. Pirotta, A. Lazaric, T. Lavril, N. Usunier, and L. Denoyer. Learning adaptive exploration strategies in dynamic environments through informed policy regularization. arXiv preprint arXiv:2005.02934, 2020. ↩
-
K. Rakelly, A. Zhou, D. Quillen, C. Finn, and S. Levine. Efficient off-policy meta-reinforcement learning via probabilistic context variables. arXiv preprint arXiv:1903.08254, 2019. ↩
-
W. R. Thompson. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3):285–294, 1933. ↩








