Selective classification, where models are allowed to “abstain” when they are uncertain about a prediction, is a useful approach for deploying models in settings where errors are costly. For example, in medicine, model errors can have life-or-death ramifications, but abstentions can be easily handled by backing off to a doctor, who then makes a diagnosis. Across a range of applications from vision ¹²³ and NLP ⁴⁵, even simple selective classifiers, relying only on model logits, routinely and often dramatically improve accuracy by abstaining. This makes selective classification a compelling tool for ML practitioners ⁶⁷.

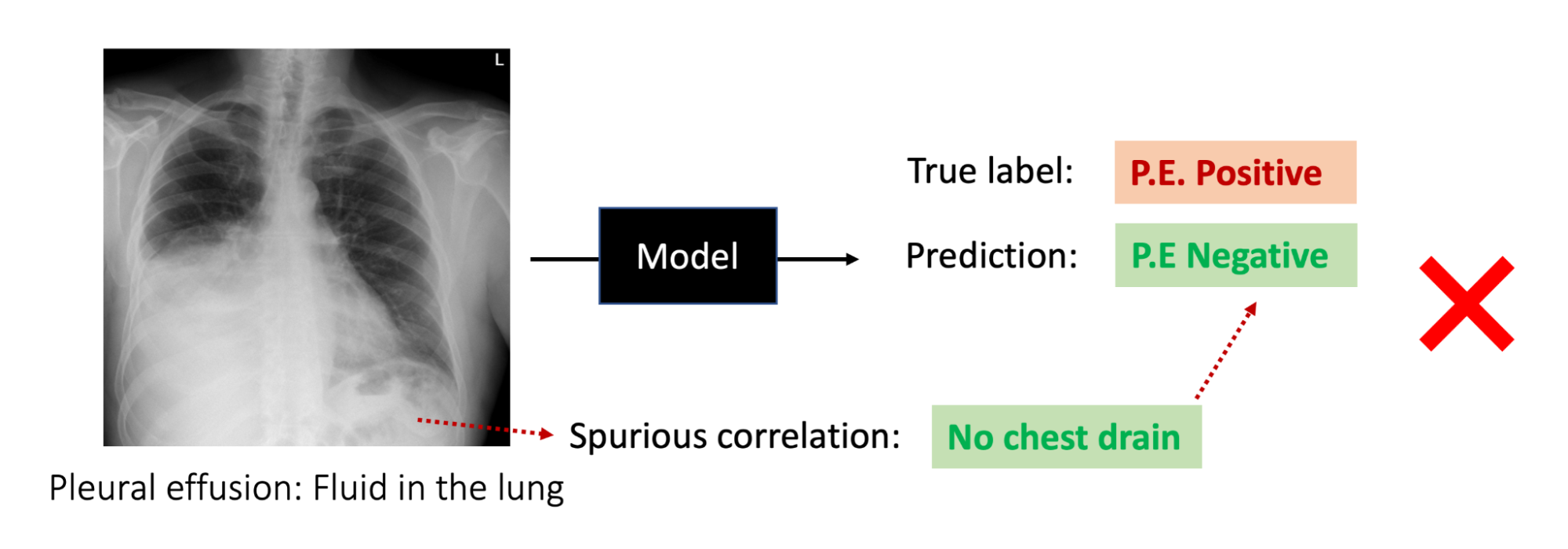
However, in our recent ICLR paper, we find that despite reliably improving average accuracy, selective classification can fail to improve and even hurt the accuracy over certain subpopulations of the data. As a motivating example, consider the task of diagnosing pleural effusion, or fluid in the lungs, from chest X-rays. Pleural effusion is often treated with a chest drain, so many pleural effusion cases also have chest drains, while most cases without pleural effusion do not have chest drains ⁸. While selective classification improves average accuracy for this task, we find that it does not appreciably improve accuracy on the most clinically relevant subgroup, or subpopulation, of the data: those that have pleural effusion but don’t yet have a chest drain, i.e. those that have pleural effusion but have not yet been treated for it. Practitioners, thus, should be wary of these potential failure modes of using selective classification in the wild.

Example of the spurious correlation setup. This patient has a pleural effusion (excess fluid in the lung), but does not yet have a chest drain. The model, relying on the presence of a chest drain to make a prediction, incorrectly predicts negative.

To further outline this critical failure mode of selective classification, we’ll first provide an overview of selective classification. We then demonstrate empirically that selective classification can hurt or fail to significantly improve accuracy on certain subgroups of the data. We next outline our theoretical results, which suggest that selective classification is rarely a good tool to resolve differences in accuracy between subgroups. And finally, suggest methods for building more equitable selective classifiers.

Selective classification basics

Imagine you are trying to build a model that classifies X-rays as either pleural effusion positive or negative. With standard classification, the model is required to either output positive or negative on each input. In contrast, a selective classifier can additionally abstain from making a prediction when it is not sufficiently confident in any class ⁹¹⁰¹¹. By abstaining, selective classifiers aim to avoid making predictions on examples they are likely to classify incorrectly, say a corrupted or difficult-to-classify X-ray, which increases their average accuracy.

Selective classification pipeline. The model makes the incorrect prediction of negative. However, the outputted confidence of 0.7 is less than the confidence threshold of 0.8, so the selective classifier abstains. Selective classifiers increase accuracy by abstaining on examples they would get wrong.

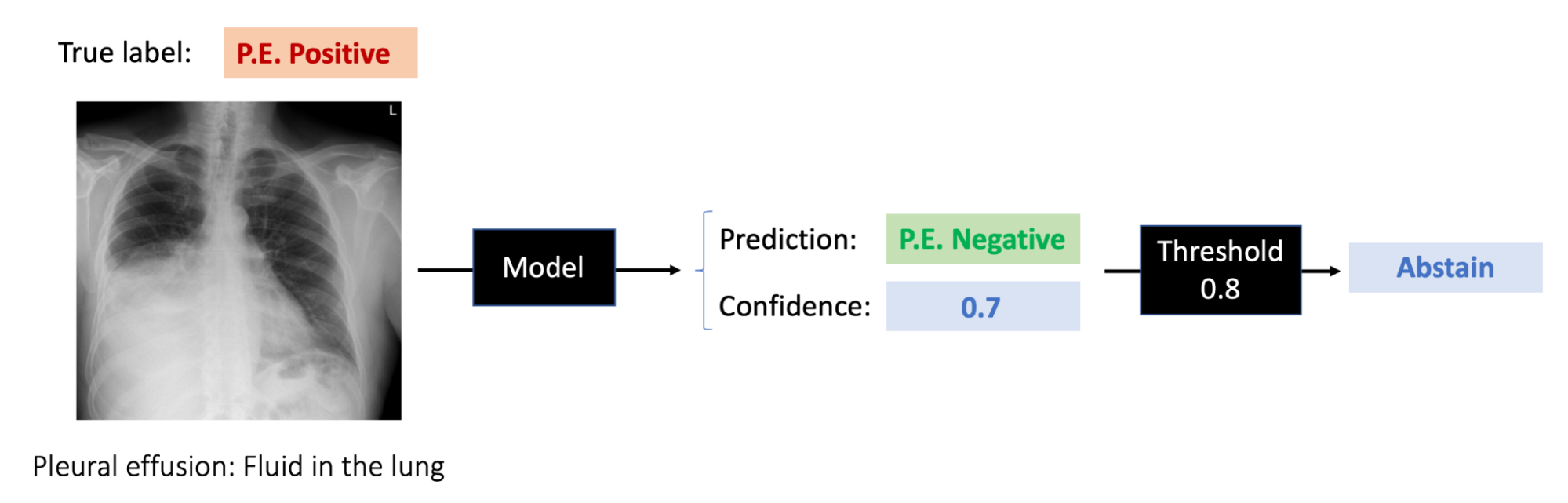
One key question in selective classification is how to choose which examples to abstain on. Selective classifiers can be viewed as two models: one that outputs a prediction (say, negative), and another that outputs a confidence in that prediction (say, 0.7 out of 1.) Whenever the confidence is above a certain (confidence) threshold, the selective classifier outputs the original prediction; for example, if the threshold were 0.6, the selective classifier would predict negative. Otherwise, the selective classifier abstains. In our work, we primarily use softmax response ¹¹ to extract confidences: the confidence in a prediction is simply the maximum softmax probability over the possible classes.

Selective classifiers are typically measured in terms of the accuracy (also called selective accuracy) on predicted examples, and the coverage, or fraction of examples the selective classifier makes predictions on ¹². We can tweak both coverage and accuracy by adjusting the confidence threshold: a lower threshold for making predictions increases the coverage, since the model’s confidence for more examples is sufficiently high. However, this tends to lower average accuracy, as the model is less confident on average in its predictions. In contrast, higher thresholds increase confidence required to make a prediction, reducing the coverage but generally increasing average accuracy.

Typically, researchers measure the performance of selective classifiers by plotting accuracy as a function of coverage. In particular, for each possible coverage (ranging from 0: abstain on everything to 1: predict on everything) they compute the maximum threshold that achieves that coverage, and then plot the accuracy at that threshold. One particularly useful reference point is the full-coverage accuracy: the accuracy of the selective classifier at coverage 1, which is the accuracy of the regular classifier.

For five datasets, we plot the average accuracy as a function of the coverage. Reading from high coverages to low coverages (right to left), as the confidence threshold increases, accuracy reliably increases. This is expected, since the model is more confident on average in its predictions at lower coverage, so more of them tend to be correct.

Selective classification can magnify accuracy disparities between subgroups

While prior work mostly focuses on average accuracy for selective classifiers, we instead focus on the accuracy of different subgroups of the data. In particular, we focus on datasets where models often latch onto spurious correlations. For example, in the above pleural effusion task, the model might learn to predict whether or not there is a chest drain, instead of directly diagnosing pleural effusion, because chest drains are highly correlated with pleural effusion; this correlation is spurious because not all pleural effusions have a chest drain. We consider subgroups that highlight this spurious correlation: two groups for when the spurious correlation gives the correct result (positive pleural effusion with chest drain, negative pleural effusion without a chest drain), and two groups when it does not (positive pleural effusion with no chest drain, negative pleural effusion with a chest drain). As a result, a model that learns this spurious correlation obtains high accuracy for the first two subgroups, but low accuracy for the latter two.

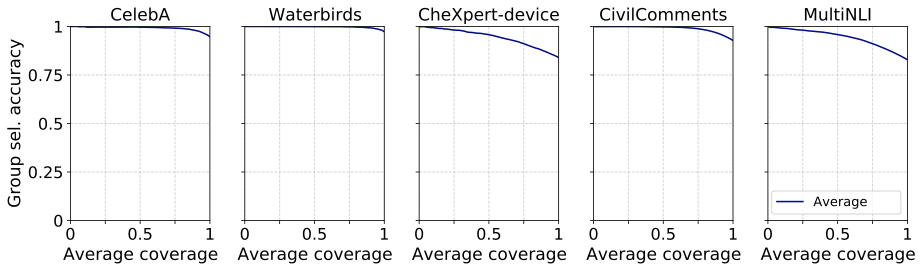
In principle, selective classification seems like a reasonable approach towards resolving these accuracy discrepancies between different subgroups of the data. Since we empirically see that selective classification reliably improves average accuracy, it must be more likely to cause a model to abstain when an example would be classified incorrectly. Incorrect examples disproportionately come from the lowest-accuracy subgroups of the data, suggesting that without bias in the confidence function, worst-group accuracy should increase faster than average accuracy.

To test this, we plot the accuracy-coverage curves over a range of tasks, including hair color classification (CelebA), bird type classification (Waterbirds), pleural effusion classification (CheXpert-device), toxicity classification (CivilComments) and natural language inference (MultiNLI). CelebA, Waterbirds, and MultiNLI use the same spurious correlation setup presented in ². CivilComments exhibits the same spurious correlations as described in the WILDS benchmark ¹³. Finally, we created the CheXpert-device dataset by subsampling the original CheXpert dataset ³ such that the presence of a chest drain even more strongly correlates with pleural effusion.

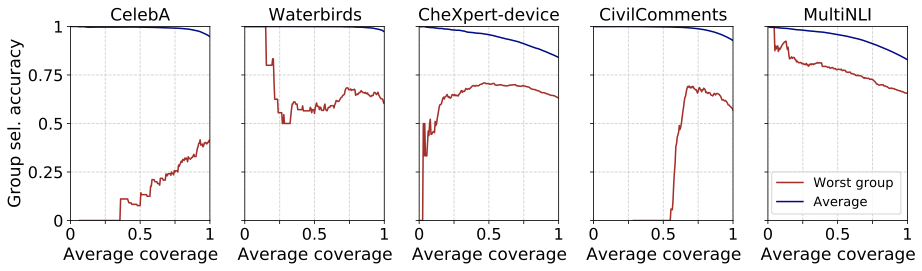
Reading from right to left, while we see that as the coverage decreases the average accuracy reliably increases, the worst-group accuracies do not always increase, and exhibit a range of undesirable behaviors. On CelebA, worst-group accuracy actually decreases: this means the more confident predictions are more likely to be incorrect. For Waterbirds, CheXpert-device, and CivilComments, worst-group accuracy sometimes increases, but never by more than 10 points until the noisy low-coverage regime, and sometimes decreases. For MultiNLI, worst-group accuracy does slowly improve, but can’t even reach 80% until very low coverages.

These results highlight that practitioners should be wary: even if selective classification reliably increases average accuracy, it will not necessarily improve the accuracy of different subgroups.

Selective classification rarely overcomes accuracy disparities

To better understand why selective classification can sometimes hurt worst-group accuracy and does not reduce full-coverage accuracy disparities, we theoretically characterize for a broad class of distributions: (1) when does selective classification improve accuracy as the confidence threshold decreases and (2) when does selective classification disproportionately help the worst group.

At a high level, our analysis focuses on the margin, or the model’s confidence for a given prediction multiplied by -1 if that prediction was incorrect. Intuitively, the more negative the margin, the “worse” the prediction. Using only the margin distribution, we can recreate the accuracy-coverage curve by abstaining on density between the negative and positive threshold, and computing the fraction of remaining density that is correct.

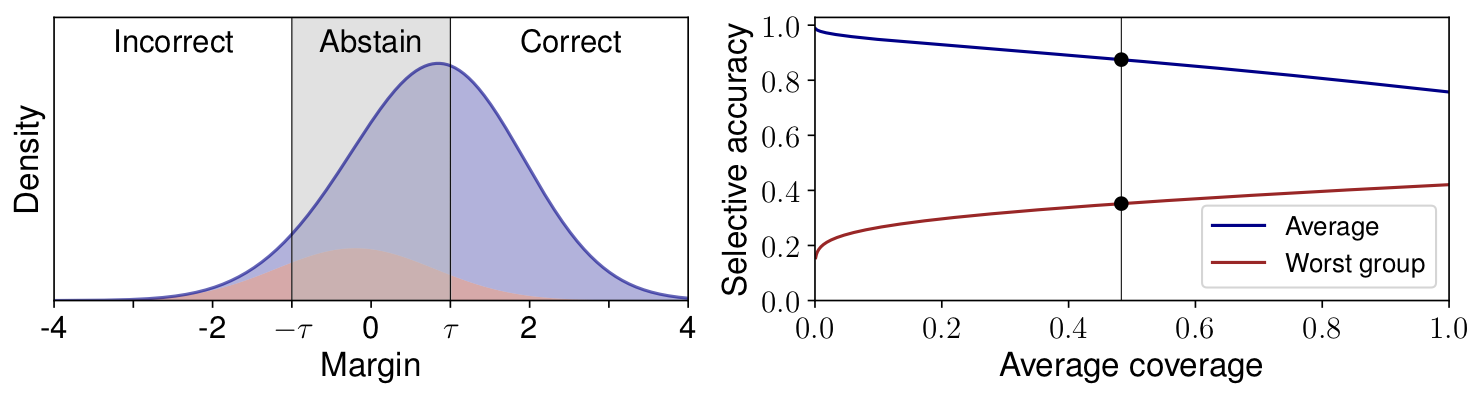
The key result of our theoretical analysis is that the full-coverage accuracy of a subgroup dramatically impacts how well selective classification performs on that subgroup, which amplifies disparities. For a wide range of margin distributions, full-coverage accuracy and a property of the margin distribution we call left-log-concavity completely determine whether or not the accuracy of a selective classifier monotonically increases or decreases. When a margin distribution is left-log-concave, which many standard distributions (e.g. gaussians) are, accuracy monotonically increases when full-coverage accuracy is at least 50% and decreases otherwise.

Next steps

So far, we have painted a fairly bleak picture of selective classification: even though it reliably improves average accuracy, it can, both theoretically and empirically, exacerbate accuracy disparities between subgroups. There are still, however, mechanisms to improve selective classification, which we outline below.

One natural step towards improving selective classification is to develop confidence functions that allow selective classifiers to overcome accuracy disparities between groups. In our paper, we test the two most widely used methods: softmax response and Monte Carlo dropout ¹⁰. We consistently find that both are disproportionately overconfident on incorrect examples from the worst-groups. However, new confidence functions that are better calibrated across groups would likely resolve disparities ¹⁴, and is an important direction for future work.

In the short term, however, we find that the most promising method to improve worst-group accuracy with selective classification is to build selective classifiers on top of already-equitable models, or models that achieve similar full-coverage accuracies across the relevant subgroups. One method to train such models is group DRO, which minimizes the maximum loss over subgroups ². We find empirically that selective classifiers trained with group DRO improve the accuracy of subgroups at roughly the same rate when they have the same accuracy at full coverage. However, group DRO is far from a perfect fix – it requires a priori knowledge of the relevant subgroups, and subgroup labels for each training example which may be costly to obtain. Nevertheless, it is a promising start, and developing more broadly applicable methods for training already-equitable models is a critical area for future work.

To conclude, despite the intuition that selective classification should improve worst-group accuracy, and selective classification’s ability to consistently improve average accuracy, common selective classifiers can severely exacerbate accuracy discrepancies between subgroups. We hope our work encourages practitioners to apply selective classification with caution, and in general focus on how different methods affect different subgroups of the data.

Acknowledgements

Thanks to the SAIL blog editors, Pang Wei Koh, and Shiori Sagawa for their helpful feedback on this blog post. This post is based off our ICLR 2021 paper:

Selective Classification Can Magnify Disparities Across Groups. Erik Jones*, Shiori Sagawa* Pang Wei Koh*, Ananya Kumar, and Percy Liang. ICLR 2021.

1. Ziwei Liu, Ping Luo, Xiaogang Wang, and Xiaoou Tang. Deep learning face attributes in the wild. In Proceedings of the IEEE International Conference on Computer Vision, pp. 3730–3738, 2015. ↩

2. Shiori Sagawa, Pang Wei Koh, Tatsunori B. Hashimoto, and Percy Liang. Distributionally robust neural networks for group shifts: On the importance of regularization for worst-case generalization. In International Conference on Learning Representations (ICLR), 2020. ↩ ↩² ↩³

3. Jeremy Irvin, Pranav Rajpurkar, Michael Ko, Yifan Yu, Silviana Ciurea-Ilcus, Chris Chute, Henrik Marklund, Behzad Haghgoo, Robyn Ball, Katie Shpanskaya, et al. Chexpert: A large chest radiograph dataset with uncertainty labels and expert comparison. In Association for the Advancement of Artificial Intelligence (AAAI), volume 33, pp. 590–597, 2019. ↩ ↩²

4. Daniel Borkan, Lucas Dixon, Jeffrey Sorensen, Nithum Thain, and Lucy Vasserman. Nuanced metrics for measuring unintended bias with real data for text classification. In World Wide Web (WWW), pp. 491–500, 2019. ↩

5. Adina Williams, Nikita Nangia, and Samuel Bowman. A broad-coverage challenge corpus for sentence understanding through inference. In Association for Computational Linguistics (ACL), pp. 1112–1122, 2018. ↩

6. Yonatan Giefman and Ran El-Yaniv. SelectiveNet: A deep neural network with an integrated reject option. In International Conference on Machine Learning (ICML), 2019. ↩

7. Hussein Mozannar and David Sontag. Consistent estimators for learning to defer to an expert. In International Conference on Machine Learning (ICML), 2020. ↩

8. Luke Oakden-Rayner, Jared Dunnmon, Gustavo Carneiro, and Christopher Ré. Hidden stratification causes clinically meaningful failures in machine learning for medical imaging. In Proceedings of the ACM Conference on Health, Inference, and Learning, pp. 151–159, 2020. ↩

9. C. K. Chow. An optimum character recognition system using decision functions. In IRE Transactions on Electronic Computers, 1957. ↩

10. Yarin Gal and Zoubin Ghahramani. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In International Conference on Machine Learning (ICML), 2016. ↩ ↩²

11. Yonatan Geifman and Ran El-Yaniv. Selective classification for deep neural networks. In Advances in Neural Information Processing Systems (NeurIPS), 2017. ↩ ↩²

12. Ran El-Yaniv and Yair Wiener. On the foundations of noise-free selective classification. Journal of Machine Learning Research (JMLR), 11, 2010. ↩

13. Pang Wei Koh, Shiori Sagawa, Henrik Marklund, Sang Michael Xie, Marvin Zhang, Akshay Balsubramani, Weihua Hu, Michihiro Yasunaga, Richard Lanas Phillips, Irena Gao, Tony Lee, Etienne David, Ian Stavness, Wei Guo, Berton A. Earnshaw, Imran S. Haque, Sara Beery, Jure Leskovec, Anshul Kundaje, Emma Pierson, Sergey Levine, Chelsea Finn, and Percy Liang. WILDS: A benchmark of in-the-wild distribution shifts. arXiv, 2020. ↩

14. Yoav Wald, Amir Feder, Daniel Greenfeld, and Uri Shalit. On Calibration and Out-of-domain Generalization. arXiv preprint arXiv:2102.10395, 2021. ↩