How heavy is an elephant? How expensive is a wedding ring?

Humans have a pretty good sense of scale, or reasonable ranges of these numeric attributes, of different objects, but do pre-trained language representations? Although pre-trained Language Models (LMs) like BERT have shown a remarkable ability to learn all kinds of knowledge, including factual knowledge, it remains unclear whether their representations can capture these types of numeric attributes from text alone without explicit training data.

In our recent paper, we measure the amount of scale information that is captured in several kinds of pre-trained text representations and show that, although generally a significant amount of such information is captured, there is still a large gap between their current performance and the theoretical upper bound. We identify that specifically those text representations that are contextual and good at numerical reasoning capture scale better. We also come up with a new version of BERT, called NumBERT, with improved numerical reasoning by replacing numbers in the pretraining text corpus with their scientific notation, which more readily exposes the magnitude to the model, and demonstrate that NumBERT representations capture scale significantly better than all those previous text representations.

Scalar Probing

In order to understand to what extent pre-trained text representations, like BERT representations, capture scale information, we propose a task called scalar probing: probing the ability to predict a distribution over values of a scalar attribute of an object. In this work, we focus specifically on three kinds of scalar attributes: weight, length, and price.

Here is the basic architecture of our scalar probing task:

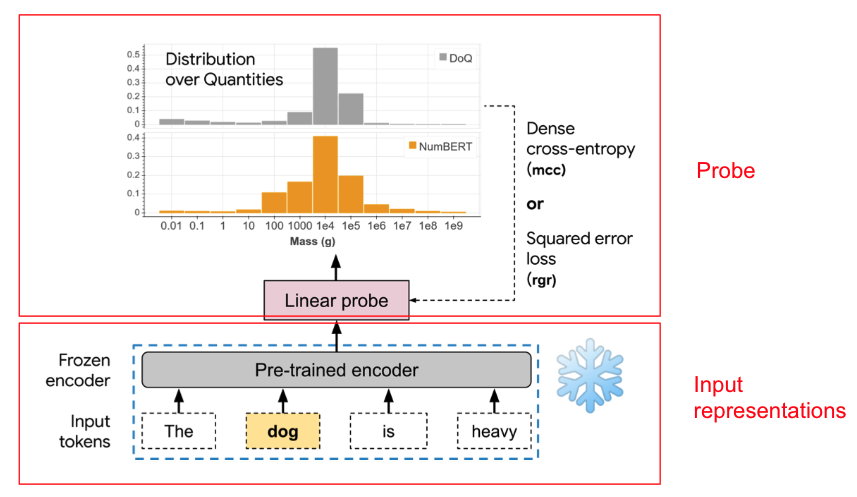
In this example, we are trying to see whether the representation of “dog” extracted by a pre-trained encoder can be used to predict/recover the distribution of the weight of a dog through a linear model. We probe three baseline language representations: Word2vec, ELMo, and BERT. Since the latter two are contextual representations that operate on sentences instead of words, we feed in sentences constructed using fixed templates. For example, for weight, we use the template “The X is heavy”, where X is the object in interest.

We explore the kind of probe that predicts a point estimate of the value and the kind that predicts the full distribution. For predicting a point estimate, we use a standard linear ReGRession (we denote as “rgr”) trained to predict the log of the median of all values for each object for the scale attribute under consideration. We predict the log because, again, we care about the general scale rather than the exact value. The loss is calculated using the prediction and the log of the median of the ground-truth distribution. For predicting the full distribution, we use a linear softmax Multi-Class Classifier (we denote as “mcc”) producing a categorical distribution over the 12 orders of magnitude. The categorical distribution predicted using the NumBERT (our improved version of BERT; will be introduced later) representations is shown as the orange histogram in the above example.

The ground-truth distributions we use come from the Distributions over Quantities (DoQ) dataset which consists of empirical counts of scalar attribute values associated with >350K nouns, adjectives, and verbs over 10 different attributes, automatically extracted from a large web text corpus. Note that during the construction of the dataset, all units for a certain attribute are first unified to a single one (e.g. centimeter/meter/kilometer -> meter) and the numeric values are scaled accordingly. We convert the collected counts for each object-attribute pair in DoQ into a categorical distribution over 12 orders of magnitude. In the above example of the weight of a dog, the ground-truth distribution is shown as the grey histogram, which is concentrated around 10-100kg.

The better the predictive performance is across all the object-attribute pairs we are dealing with, the better the pre-trained representations encode the corresponding scale information.

NumBERT

Before looking at the scalar probing results of these different language presentations, let’s also think about what kind of representations might be good at capturing scale information and how to improve existing LMs to capture scale better. All of these models are trained using large online text corpora like Wikipedia, news, etc. How can their representations pick up scale information from all this text?

Here is a piece of text from the first document I got when I searched on Google “elephant weight”:

“…African elephants can range from 5,000 pounds to more than 14,000 pounds (6,350 kilograms)…”

So it is highly likely that the learning of scale is partly mediated by the transfer of scale information from the numbers (here “5,000”, “14,000”, etc.) to nouns (here “elephants”) and numeracy, i.e. the ability to reason about numbers, is probably important for representing scale!

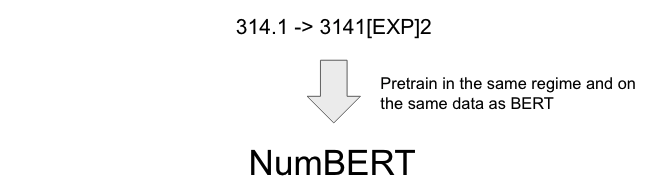
However, previous work has shown that existing pre-trained text representations, including BERT, ELMo, and Word2Vec, are not good at reasoning over numbers. For example, beyond the magnitude of ~500, they cannot even decode a number from its word embedding, e.g. embedding(“710”) \(\nrightarrow\) 710. Thus, we propose to improve the numerical reasoning abilities of these representations by replacing every instance of a number in the LM training data with its scientific notation, and re-pretraining BERT (which we call NumBERT). This enables the model to more easily associate objects in the sentence directly with the magnitude expressed in the exponent, ignoring the relatively insignificant mantissa.

Results

Scalar Probing

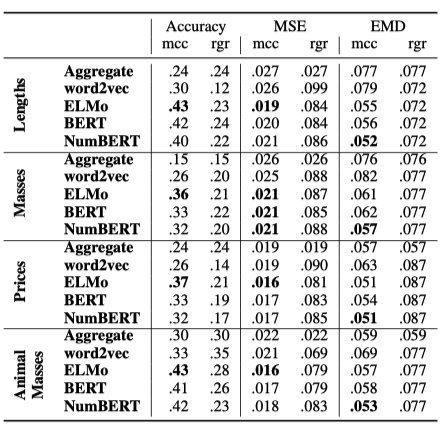
The above table shows the results of scalar probing on the DoQ data. We use three evaluation metrics: Accuracy, Mean Squared Error (MSE), and Earth Mover’s distance (EMD), and we do the experiments in four domains: Lengths, Masses, Prices and Animal Masses (a subset of Masses). For MSE and EMD, the best possible score is 0, while we compute a loose upper bound of accuracy by sampling from the ground-truth distribution and evaluating against the mode. This upper bound achieves accuracies of 0.570 for lengths, 0.537 for masses, and 0.476 for prices.

For the Aggregate baseline, for each attribute, we compute the empirical distribution over buckets across all objects in the training set, and use that as the predicted distribution for all objects in the test set. Compared with this baseline, we can see that the mcc probe over the best text representations capture about half (as measured by accuracy) to a third (by MSE and EMD) of the distance to the upper bound mentioned above, suggesting that while a significant amount of scalar information is available, there is a long way to go to support robust commonsense reasoning.

Specifically, NumBERT representations do consistently better than all the others on Earth Mover’s Distance (EMD), which is the most robust metric because of its better convergence properties and robustness to adversarial perturbations of the data distribution. Word2Vec performs significantly worse than the contextual representations – even though the task is noncontextual (since we do not have different ground-truths for an object occurring in different contexts in our setting). Also, despite being weaker than BERT on downstream NLP tasks, ELMo does better on scalar probing, consistent with it being better at numeracy due to its character-level tokenization.

Zero-shot transfer

We note that DoQ is derived heuristically from web text and contains noise. So we also evaluate probes trained on DoQ on 2 datasets containing ground truth labels of scalar attributes: VerbPhysics and Amazon Price Dataset. The first is a human labeled dataset of relative comparisons, e.g. (person, fox, weight, bigger). Predictions for this task are made by comparing the point estimates for rgr and highest-scoring buckets for mcc. The second is a dataset of empirical distributions of product prices on Amazon. We retrained a probe on DoQ prices using 12 power-of-4 buckets to support finer grained predictions.

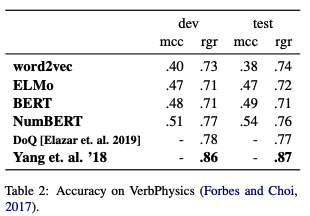
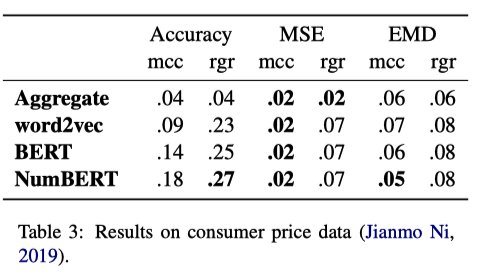
The results are shown in the tables above. On VerbPhysics (the table on the top), rgr+NumBERT performed best, approaching the performance of using DoQ as an oracle, though short of specialized models for this task. Scalar probes trained with mcc perform poorly, possibly because a finer-grained model of predicted distribution is not useful for the 3-class comparative task. On the Amazon Price Dataset (the table on the bottom) which is a full distribution prediction task, mcc+NumBERT did best on both distributional metrics. On both zero-shot transfer tasks, NumBERT representations were the best across all configurations of metrics/objectives, suggesting that manipulating numeric representations of the text in the pre-training corpora can significantly improve performance on scale prediction.

Moving Forward

In the work above, we introduce a new task called scalar probing used to measure how much information of numeric attributes of objects pre-trained text representations have captured and find out that while there is a significant amount of scale information in object representations (half to a third to the theoretical upper bound), these models are far from achieving common sense scale understanding. We also come up with an improved version of BERT, called NumBERT, whose representations capture scale information significantly better than all the previous ones.

Scalar probing opens up new exciting research directions to explore. For example, lots of work has pre-trained large-scale vision & language models, like ViLBERT and CLIP. Probing their representations to see how much scale information has been captured and performing systematic comparisons between them and representations learned by language-only models can be quite interesting.

Also, models learning text representations that predict scale better can have a great real-world impact. Consider a web query like:

“How tall is the tallest building in the world?”

With a common sense understanding of what a reasonable range of heights for “building” is, we can detect errors in the current web QA system when there are mistakes in retrieval or parsing, e.g. when a wikipedia sentence about a building is mistakenly parsed as being 19 miles high instead of meters.

Check out the paper Do Language Embeddings Capture Scales? by Xikun Zhang, Deepak Ramachandran, Ian Tenney, Yanai Elazar, and Dan Roth.