In this post, we provide a Bayesian inference framework for in-context learning in large language models like GPT-3 and show empirical evidence for our framework, highlighting the differences from traditional supervised learning. This blog post primarily draws from the theoretical framework for in-context learning from An Explanation of In-context Learning as Implicit Bayesian Inference 1 and experiments from Rethinking the Role of Demonstrations: What Makes In-Context Learning Work? 2.
TL;DR – In-context learning is a mysterious emergent behavior in large language models (LMs) where the LM performs a task just by conditioning on input-output examples, without optimizing any parameters. In this post, we provide a Bayesian inference framework for understanding in-context learning as “locating” latent concepts the LM has acquired from pretraining data. This suggests that all components of the prompt (inputs, outputs, formatting, and the input-output mapping) can provide information for inferring the latent concept. We connect this framework to empirical evidence where in-context learning still works when provided training examples with random outputs. While output randomization cripples traditional supervised learning algorithms, it only removes one source of information for Bayesian inference (the input-output mapping). Finally, we present missing gaps and avenues for future work and invite the community to join us in further understanding in-context learning.
Content
- The mystery of in-context learning
- A framework for in-context learning
- Empirical evidence
- Avenues for extensions
- Wrapping up
The mystery of in-context learning
Large language models (LMs) such as GPT-3 3 are trained on internet-scale text data to predict the next token given the preceding text. This simple objective paired with a large-scale dataset and model results in a very flexible LM that can “read” any text input and condition on it to “write” text that could plausibly come after the input. While the training procedure is both simple and general, the GPT-3 paper found that the large scale leads to a particularly interesting emergent behavior 4 called in-context learning.
What is in-context learning? In-context learning was popularized in the original GPT-3 paper as a way to use language models to learn tasks given only a few examples.[1] During in-context learning, we give the LM a prompt that consists of a list of input-output pairs that demonstrate a task. At the end of the prompt, we append a test input and allow the LM to make a prediction just by conditioning on the prompt and predicting the next tokens. To correctly answer the two prompts below, the model needs to read the training examples to figure out the input distribution (financial or general news), output distribution (Positive/Negative or topic), input-output mapping (sentiment or topic classification), and the formatting.

What can in-context learning do? On many benchmark NLP benchmarks, in-context learning is competitive with models trained with much more labeled data and is state-of-the-art on LAMBADA (commonsense sentence completion) and TriviaQA (question answering). Perhaps even more exciting is the array of applications that in-context learning has enabled people to spin up in just a few hours, including writing code from natural language descriptions, helping with app design mockups, and generalizing spreadsheet functions:
Here's a sentence describing what Google's home page should look and here's GPT-3 generating the code for it nearly perfectly. pic.twitter.com/m49hoKiEpR
— Sharif Shameem (@sharifshameem) July 15, 2020
This changes everything. 🤯
— jordan singer (@jsngr) July 18, 2020
With GPT-3, I built a Figma plugin to design for you.
I call it "Designer" pic.twitter.com/OzW1sKNLEC
=GPT3()... the spreadsheet function to rule them all.
— Paul Katsen (@pavtalk) July 21, 2020
Impressed with how well it pattern matches from a few examples.
The same function looked up state populations, peoples' twitter usernames and employers, and did some math. pic.twitter.com/W8FgVAov2f
In-context learning allows users to quickly build models for a new use case without worrying about fine-tuning and storing new parameters for each task. It typically requires very few training examples to get a prototype working, and the natural language interface is intuitive even for non-experts.
Why is in-context learning surprising? In-context learning is unlike conventional machine learning in that there’s no optimization of any parameters. However, this isn’t unique—meta-learning methods have trained models that learn from examples 5. The mystery is that the LM isn’t trained to learn from examples. Because of this, there’s seemingly a mismatch between pretraining (what it’s trained to do, which is next token prediction) and in-context learning (what we’re asking it to do).
This seems like magic. How does in-context learning work?
A framework for in-context learning
How can we better understand in-context learning? The first thing to note is that a large LM like GPT-3 has been trained on a massive amount of text with a wide array of topics and formats, from Wikipedia pages, academic papers, and Reddit posts to Shakespeare’s works. We hypothesize that training on this text allows the LM to model a diverse set of learned concepts.
In Xie et al., we propose a framework in which the LM uses the in-context learning prompt to “locate” a previously learned concept to do the in-context learning task. For example (see figure below), in our framework, the LM uses the training examples to internally figure out that the task is either sentiment analysis (left) or topic classification (right) and apply the same mapping to the test input.

What’s a concept? We can think of a concept as a latent variable that contains various document-level statistics. For example, a “news topics” concept describes a distribution of words (news and their topics), a format (the way that news articles are written), a relation between news and topics, and other semantic and syntactic relationships between words. In general, concepts may be a combination of many latent variables that specify different aspects of the semantics and syntax of a document, but we simplify here by grouping them all into one concept variable.
How does the LM learn to do Bayesian inference during pretraining?
We show that an LM trained (using next token prediction) on synthetic data with a latent concept structure can learn to do in-context learning. We hypothesize that a similar effect can occur in real pretraining data since text documents naturally have long-term coherence: sentences/paragraphs/table rows in the same document tend to share underlying semantic information (e.g., topic) and formatting (e.g., a FAQ page alternates between questions and answers). In our framework, the document-level latent concept creates long-term coherence, and modeling this coherence during pretraining requires learning to infer the latent concept:
- Pretrain: To predict the next token during pretraining, the LM must infer (“locate”) the latent concept for the document using evidence from the previous sentences.
- In-context learning: If the LM also infers the prompt concept (the latent concept shared by examples in the prompt) using in-context examples in the prompt, then in-context learning occurs!
Bayesian inference view of in-context learning
Before we get into the Bayesian inference view, let’s set up the in-context learning setting.
-
Pretraining distribution (\(p\)): Our main assumption on the structure of pretraining documents is that a document is generated by first sampling a latent concept, and then the document is generated by conditioning on the latent concept. We assume that the pretraining data and LM are large enough that the LM fits the pretraining distribution exactly. Because of this, we will use \(p\) to denote both the pretraining distribution and the probability under the LM.
-
Prompt distribution: In-context learning prompts are lists of IID (independent and identically distributed) training examples concatenated together with one test input. Each example in the prompt is drawn as a sequence conditioned on the same prompt concept, which describes the task to be learned.
The process of “locating” learned capabilities can be viewed as Bayesian inference of a prompt concept that every example in the prompt shares. If the model can infer the prompt concept, then it can be used to make the correct prediction on the test example. Mathematically, the prompt provides evidence for the model (\(p\)) to sharpen the posterior distribution over concepts, \(p(\text{concept} \mid \text{prompt})\). If \(p(\text{concept} \mid \text{prompt})\) is concentrated on the prompt concept, the model has effectively “learned” the concept from the prompt.
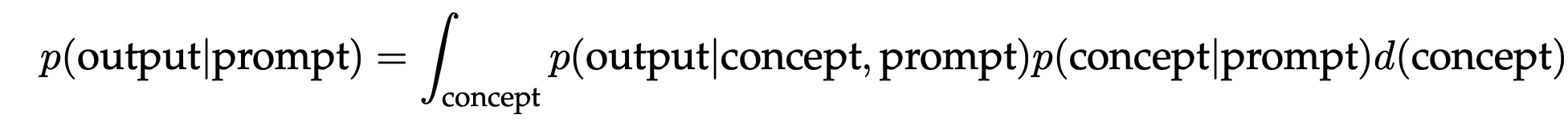
Ideally, \(p(\text{concept} \mid \text{prompt})\) concentrates on the prompt concept with more examples in the prompt so that the prompt concept is “selected” through marginalization.
Prompts provide noisy evidence for Bayesian inference
The logical leap in the explanation is that the LM will infer the prompt concept from in-context examples, even though prompts are sampled from the prompt distribution, which can be very different from the pretraining distribution that the LM trained on. Prompts concatenate independent training examples together, so the transitions between examples can be very low-probability under the LM (and the pretraining distribution), and can introduce noise into the inference process. For example, concatenating independent sentences about different news topics may result in very atypical text, since none of the sentences have sufficient context. Interestingly, the LM can still do Bayesian inference despite the mismatch between the pretraining and prompt distributions, as seen empirically in GPT-3. We prove that in-context learning via Bayesian inference can emerge from latent concept structure in the pretraining data in a simplified theoretical setting and use this to generate a synthetic dataset where in-context learning emerges for both Transformers and LSTMs.

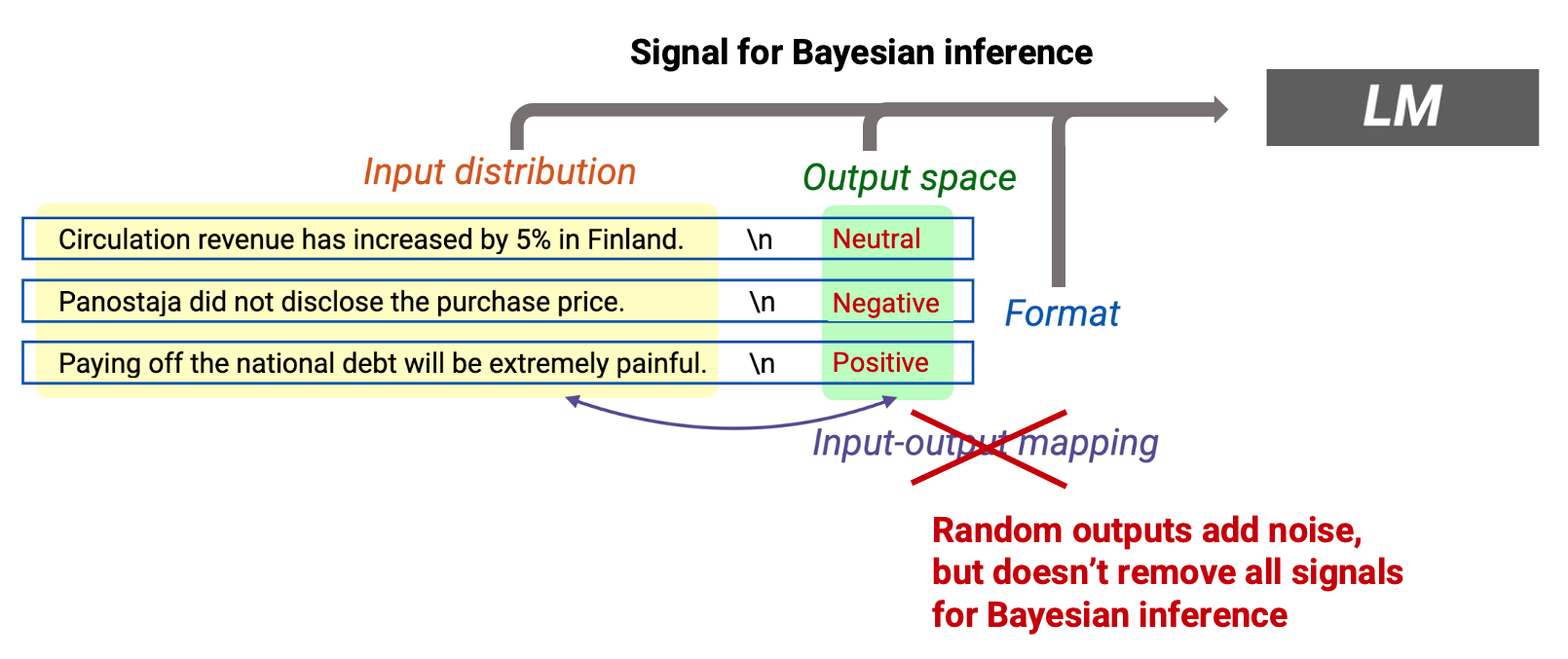
Training examples provide signal: We can think of the training examples as providing a signal for Bayesian inference. In particular, the transitions within training examples (green in the figure above) allow the LM to infer the latent concept they all share. In a prompt, the green transitions come from the input distribution (the transitions inside the news sentence), the output distribution (the topic word), the format (syntax of news sentence), and the input-output mapping (relation between the news and the topic) all provide signal for Bayesian inference.
Transitions between training examples can be low-probability (noise): Because the training examples are IID, concatenating them together often creates unnatural, low-probability transitions between examples. For example, seeing a sentence about the NFC Championship after a sentence about circulation revenue in Finland may be surprising (see figure above). These transitions create noise in the inference process, and stems from the mismatch between the pretraining and prompt distributions.
In-context learning is robust to some noise: We prove that if the signal is greater than the noise, then the LM can successfully do in-context learning: it predicts the correct test output as the number of training examples (\(n\)) goes to infinity.[2] We characterize the signal as the KL divergence between other concepts and the prompt concept conditioned on the prompt, and the noise as error terms coming from the transitions between examples. Intuitively, if the prompt allows the model to distinguish the prompt concept from other concepts really easily, then there’s a strong signal.[3] This also suggests that with a strong enough signal, other forms of noise such as removing a source of information (e.g., input-output mapping) could be tolerable, especially if the format of the prompt doesn’t change and the input-output mapping information is in the pretraining data. This is different from traditional supervised learning, which would fail if the input-output mapping information is removed (e.g., by randomizing the labels). We will examine this distinction directly in the next section.
Small-scale testbed for in-context learning (GINC dataset): To support the theory, we built GINC, a synthetic pretraining dataset and in-context learning testbed with the latent concept structure. We found that pretraining on GINC causes in-context learning to emerge for both Transformers and LSTMs, suggesting that the main effect comes from the structure in the pretraining data. Ablations show that the latent concept structure (which leads to long-term coherence) is crucial for the emergence of in-context learning in GINC (see Xie et al. to learn more).
Empirical evidence
Next, we aim to provide empirical evidence for the above framework through a set of experiments.
Input-output pairing in the prompt matters much less than previously thought
tl;dr: Forming the prompt with the ground truth output is not required to achieve good in-context learning performance.[4]
In Min et al., we compare three different methods:
- No-examples: the LM conditions on the test input only, with no examples. This is typical zero-shot inference, first done by GPT-2/GPT-3.
- Examples with ground truth outputs: the LM conditions on the concatenation of a few in-context examples and the test input. This is a typical in-context learning method, and by default, all outputs in the prompt are ground truth.
- Examples with random outputs: the LM conditions on in-context examples and the test input, but now, each output in the prompt is randomly sampled from the output set (labels in the classification tasks; a set of answer options in the multi-choice tasks).


In particular, the approach “Examples with random outputs” hasn’t been tried before. Typical supervised learning will not work at all if the outputs of the labeled data are random, since the task does not make sense anymore.
We experiment with 12 models whose sizes range from 774M to 175B, including the largest GPT-3 (Davinci). Models are evaluated on 16 classification datasets and 10 multi-choice datasets.
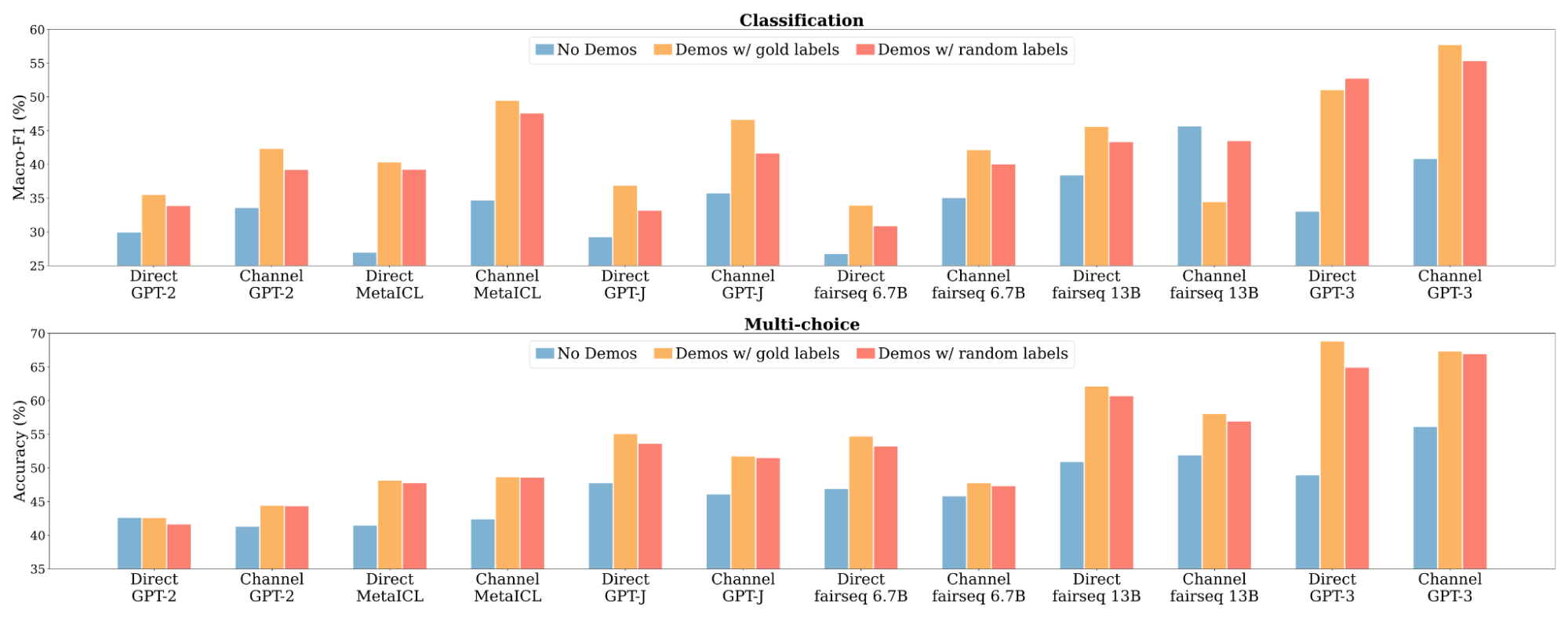
In-context learning performance does not drop much when each output is replaced with a random output from the output set.
First, as expected, using the examples with ground truth outputs significantly outperforms no-examples. Then, replacing ground truth outputs with random outputs only barely hurts performance. This means, unlike typical supervised learning, ground truth outputs are not really required to achieve good in-context learning performance, which is counter-intuitive!

If the correct input-output mapping has a marginal effect, which aspects of the prompt are most important for in-context learning?
One possible aspect is the input distribution, i.e., the underlying distribution that inputs in the examples are from (the red text in the figure below). To quantify its impact, we design a variant of demonstrations where each in-context example consists of an input sentence that is randomly sampled from an external corpus (instead of the input from the training data). We then compare its performance with demonstrations with random labels. The intuition is that these two versions of demonstrations both do not keep the correct input-label correspondence, but only differ in whether or not the LM conditions on the correct input distribution.
Results indicate that overall, the model with random sentences as inputs achieves significantly lower performance (up to 16% absolute points worse). This indicates conditioning on the correct input distribution is important.

Another aspect that may affect in-context learning is the output space: the set of outputs (classes or answer choices) in the task. To quantify its impact, we design a variant of demonstrations consisting of in-context examples with randomly paired, random English unigrams that are not related to the original labels of the task (e.g., “wave”). Results indicate that there is a significant performance drop when using this demonstration (up to 16% absolute). This indicates conditioning on the correct output space is important.[5] This is true even for a multi-choice task, likely because it still has a particular distribution of the choices (e.g., objects like “Bolts” and “Screws” in the OpenBookQA dataset) that the model uses.
Connections to the Bayesian inference framework
The fact that the LMs do not rely on the input-output correspondence in the prompt possibly means that the LMs might have been exposed to some notions of the input-output correspondence for the task during pretraining, and in-context learning is simply relying on them. Instead, all the components of the prompt (input distribution, the output space and format) are providing “evidence” to enable the model to better infer (locate) concepts that are learned during pretraining. The random input-output mapping still increases the “noise” due to concatenating random sequences together in the prompt. Nonetheless, based on our framework, the model still does Bayesian inference as long as there is still enough signal (such as the correct input distribution, output space, and format). Of course, having the correct input-output mapping can still help by providing more evidence and reducing noise, especially when the input-output mapping doesn’t show up often in pretraining data.
In-context learning performance is highly correlated with term frequencies during pretraining
Razeghi et al. 6 evaluate GPT-J on various numeric tasks, and find that in-context learning performance is highly correlated with how many times the terms in each instance (numbers and units) appear in the pretraining data of GPT-J (The PILE).
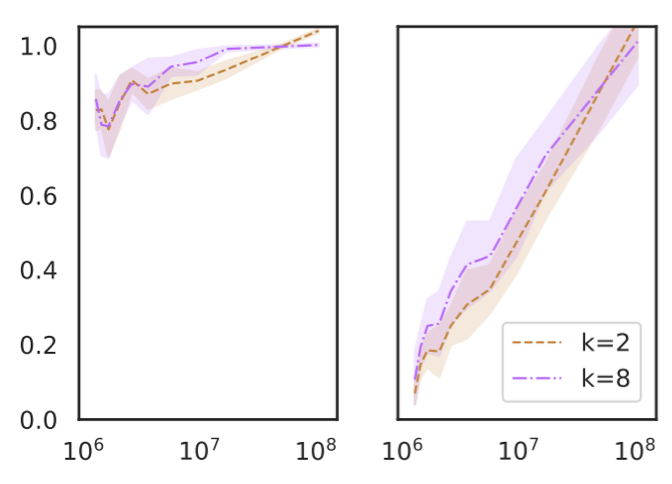
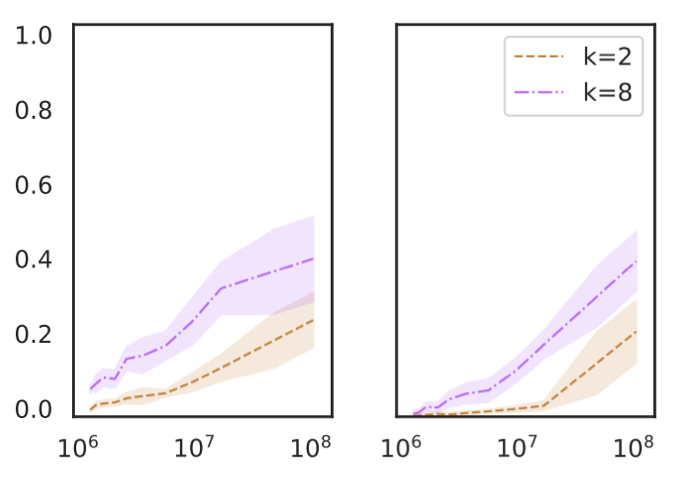
This is consistent across different types of numeric tasks (addition, multiplication and unit conversions), and different values of k (the number of labeled examples in the prompt). An interesting fact is that this is true also when the input does not explicitly state the task—for instance, instead of using “Q: What is 3 times 4? A: 12”, use “Q: What is 3 # 4? A: 12”.
Connections to the Bayesian inference framework
We view this work as another piece of evidence that shows in-context learning is mainly about locating latent concepts learned during pretraining. In particular, if terms in a particular instance are exposed many times in the pretraining data, the model is likely to know better about the distribution of the inputs. This will provide better evidence to locate latent concepts to perform a downstream task, according to Bayesian inference. While Razeghi et al. specifically focuses on one aspect of how much the model would know the input distribution — term frequencies of the specific instance — there can be a broader set of variations, such as frequencies of the input-output correlation, the format (or the text pattern), and more.
Avenues for extensions
Understanding model performance on “unseen” tasks
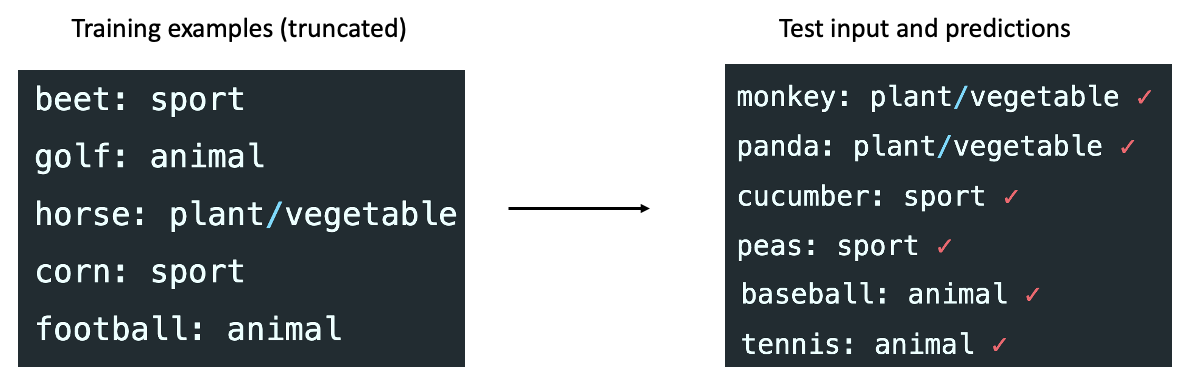
Our framework suggests that the model is “localizing” or “retrieving” concepts that it has learned during pretraining. However, Rong shows in this blog post that the model performs almost perfectly on an unnatural/unseen synthetic task that maps sports to animals, vegetables to sports, etc (below). Also, the input-output mapping still matters in this case since the model learns the unnatural mapping from examples. Empirically, one possibility is that in-context learning behaviors may change in synthetic tasks (rather than real NLP benchmarks that our experiments focus on) – this requires further investigation.
Nonetheless, Bayesian inference could still explain some forms of extrapolation if we view a concept as a composition of many latent variables. For example, consider a latent variable representing syntax and another variable representing semantics. Bayesian inference can combinatorially generalize to new semantics-syntax pairs even if the model has not seen all the pairs during pretraining. General operations like permutation, swapping, and copying are useful during pretraining and can help extrapolation when composed (e.g., label permutation in the sport-to-animal case). More work is needed to model how in-context learning can work on unseen tasks.
Connection to learning to read task descriptions
Task descriptions (or instructions) in natural language can be used in the prompt to perform a downstream task. For instance, we can prepend “Write a summary about the given article” to describe summarization or “Answer a following question about the Wikipedia article” to describe question answering. Language models that are further tuned on the large-scale, high-quality instruction data are shown to perform unseen tasks very well 7 8. In light of our framework, we can understand specifying the task description as improving Bayesian inference by providing explicit observations of the latent prompt concept. Extending the framework to incorporate task descriptions can inform other more compact ways of specifying the task.
Understanding pretraining data for in-context learning
While we propose that in-context learning comes from long-term coherence structure in the pretraining data (due to the latent concept structure), more work is needed to pinpoint exactly what elements of the pretraining data are the biggest contributors to in-context learning. Is there a critical subset of data from which in-context learning emerges, or is it a complex interaction between many types of data? Recent works give some hints about the kind of pretraining data needed to elicit in-context learning behaviors 9 10. A better understanding of the ingredients for in-context learning can help construct a more effective large-scale pretraining dataset.
Capturing effects from model architecture and training
Our framework only describes the effect of pretraining data on in-context learning, but there can be effects from all the other parts of the ML pipeline. Model scale is one of them—many papers have shown the benefits of scale 11 12 13. Architecture (e.g., decoder-only vs. encoder-decoder) and objective (e.g., casual LM vs. masked LM) are other factors, as Wang et al 14 investigated in depth. Future work may further investigate how the model behavior in in-context learning depends on the model scale and the choices of architecture and training objective.
Wrapping up
In this blog post, we provide a framework where the LM does in-context learning by using the prompt to “locate” the relevant concept it has learned during pretraining to do the task. We can theoretically view this as Bayesian inference of a latent concept conditioned on the prompt, and this capability comes from structure (long-term coherence) in the pretraining data. We connect this to empirical evidence on NLP benchmarks showing that in-context learning still works well when outputs in the prompt are replaced with random outputs. While random outputs add noise and remove input-output mapping information, other components (input distribution, output distribution, format) still provide evidence for Bayesian inference. Finally, we detail limitations and possible extensions of our framework, such as explaining extrapolation to unseen tasks and incorporating the effect of model architecture and optimization. We call for more future work on understanding and improving in-context learning.
Acknowledgements
We thank Rishi Bommasani, Gabriel Ilharco, Jungo Kasai, Ananya Kumar, Percy Liang, Tengyu Ma, Ofir Press, Yasaman Razeghi, Megha Srivastava, Luke Zettlemoyer, and Michael Zhang for their comments and suggestions on the blog post.
[1] Another definition of in-context learning from Kaplan et al. is that the model improves at predicting the next token when given progressively more preceding context. In this post, we focus on the few-shot task learning view of in-context learning. ↩
[2] In the theory, we assume that a concept is a hidden state transition matrix for a Hidden Markov Model (HMM) and a document is generated by first sampling a concept from a family of concepts, then sampling a sequence from an HMM with the concept as the transition matrix. Intuitively, the transition matrix describes a distribution of words (through likely hidden states) and their relationships, which can describe the task. ↩
[3] Longer example lengths improve asymptotic error: Interestingly, we also prove that increasing the length of the example (let’s call it \(k\)) decreases the asymptotic error, while increasing the number of examples (\(n\)) gets us closer to the asymptotic error. Intuitively, with longer examples, there are a lot more green arrows than red ones, and the amount of signal dominates the noise.↩
[4] The original paper uses the term “demonstrations” to refer to the in-context examples in the prompt.↩
[5] The channel model that computes the probability of the input conditioned on the output (instead of the probability of the output conditioned on the input) has an exception, which is likely because the inference formulation makes the model largely insensitive to the output space.↩
-
Sang Michael Xie, Aditi Raghunathan, Percy Liang, Tengyu Ma. An Explanation of In-context Learning as Implicit Bayesian Inference. International Conference on Learning Representations (ICLR), 2022. ↩
-
Sewon Min, Xinxi Lyu, Ari Holtzman, Mikel Artetxe, Mike Lewis, Hannaneh Hajishirzi, Luke Zettlemoyer. Rethinking the Role of Demonstrations: What Makes In-Context Learning Work? arXiv preprint, 2022. ↩
-
Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, Dario Amodei. Language Models are Few-Shot Learners. Neural Information Processing Systems (NeurIPS), 2020. ↩
-
Jason Wei, Yi Tay, Rishi Bommasani, Colin Raffel, Barret Zoph, Sebastian Borgeaud, Dani Yogatama, Maarten Bosma, Denny Zhou, Donald Metzler, Ed H. Chi, Tatsunori Hashimoto, Oriol Vinyals, Percy Liang, Jeff Dean, William Fedus. Emergent Abilities of Large Language Models. arXiv preprint, 2022. ↩
-
Sachin Ravi and Hugo Larochelle. Optimization as a model for few-shot learning. In International Conference on Learning Representations (ICLR), 2017. ↩
-
Yasaman Razeghi, Robert L. Logan IV, Matt Gardner, Sameer Singh. Impact of Pretraining Term Frequencies on Few-Shot Reasoning. arXiv preprint, 2022. ↩
-
Jason Wei, Maarten Bosma, Vincent Y. Zhao, Kelvin Guu, Adams Wei Yu, Brian Lester, Nan Du, Andrew M. Dai, Quoc V. Le. Finetuned Language Models Are Zero-Shot Learners. International Conference on Learning Representations (ICLR), 2022. ↩
-
Victor Sanh, Albert Webson, Colin Raffel, Stephen H. Bach, Lintang Sutawika, Zaid Alyafeai, Antoine Chaffin, Arnaud Stiegler, Teven Le Scao, Arun Raja, Manan Dey, M Saiful Bari, Canwen Xu, Urmish Thakker, Shanya Sharma Sharma, Eliza Szczechla, Taewoon Kim, Gunjan Chhablani, Nihal Nayak, Debajyoti Datta, Jonathan Chang, Mike Tian-Jian Jiang, Han Wang, Matteo Manica, Sheng Shen, Zheng Xin Yong, Harshit Pandey, Rachel Bawden, Thomas Wang, Trishala Neeraj, Jos Rozen, Abheesht Sharma, Andrea Santilli, Thibault Fevry, Jason Alan Fries, Ryan Teehan, Tali Bers, Stella Biderman, Leo Gao, Thomas Wolf, Alexander M. Rush. Multitask Prompted Training Enables Zero-Shot Task Generalization. International Conference on Learning Representations (ICLR), 2022. ↩
-
Stephanie C.Y. Chan, Adam Santoro, Andrew K. Lampinen, Jane X. Wang, Aaditya Singh, Pierre H. Richemond, Jay McClelland, Felix Hill. Data Distributional Properties Drive Emergent In-Context Learning in Transformers. arXiv preprint, 2022. ↩
-
Seongjin Shin, Sang-Woo Lee, Hwijeen Ahn, Sungdong Kim, HyoungSeok Kim, Boseop Kim, Kyunghyun Cho, Gichang Lee, Woomyoung Park, Jung-Woo Ha, Nako Sung. On the Effect of Pretraining Corpora on In-context Learning by a Large-scale Language Model. North American Chapter of the Association for Computational Linguistics (NAACL), 2022. ↩
-
Jared Kaplan, Sam McCandlish, Tom Henighan, Tom B. Brown, Benjamin Chess, Rewon Child, Scott Gray, Alec Radford, Jeffrey Wu, Dario Amodei. Scaling Laws for Neural Language Models. arXiv preprint, 2020. ↩
-
Jack W. Rae, Sebastian Borgeaud, Trevor Cai, Katie Millican, Jordan Hoffmann, Francis Song, John Aslanides, Sarah Henderson, Roman Ring, Susannah Young, Eliza Rutherford, Tom Hennigan, Jacob Menick, Albin Cassirer, Richard Powell, George van den Driessche, Lisa Anne Hendricks, Maribeth Rauh, Po-Sen Huang, Amelia Glaese, Johannes Welbl, Sumanth Dathathri, Saffron Huang, Jonathan Uesato, John Mellor, Irina Higgins, Antonia Creswell, Nat McAleese, Amy Wu, Erich Elsen, Siddhant Jayakumar, Elena Buchatskaya, David Budden, Esme Sutherland, Karen Simonyan, Michela Paganini, Laurent Sifre, Lena Martens, Xiang Lorraine Li, Adhiguna Kuncoro, Aida Nematzadeh, Elena Gribovskaya, Domenic Donato, Angeliki Lazaridou, Arthur Mensch, Jean-Baptiste Lespiau, Maria Tsimpoukelli, Nikolai Grigorev, Doug Fritz, Thibault Sottiaux, Mantas Pajarskas, Toby Pohlen, Zhitao Gong, Daniel Toyama, Cyprien de Masson d’Autume, Yujia Li, Tayfun Terzi, Vladimir Mikulik, Igor Babuschkin, Aidan Clark, Diego de Las Casas, Aurelia Guy, Chris Jones, James Bradbury, Matthew Johnson, Blake Hechtman, Laura Weidinger, Iason Gabriel, William Isaac, Ed Lockhart, Simon Osindero, Laura Rimell, Chris Dyer, Oriol Vinyals, Kareem Ayoub, Jeff Stanway, Lorrayne Bennett, Demis Hassabis, Koray Kavukcuoglu, Geoffrey Irving. Scaling Language Models: Methods, Analysis & Insights from Training Gopher. arXiv preprint, 2022. ↩
-
Aakanksha Chowdhery, Sharan Narang, Jacob Devlin, Maarten Bosma, Gaurav Mishra, Adam Roberts, Paul Barham, Hyung Won Chung, Charles Sutton, Sebastian Gehrmann, Parker Schuh, Kensen Shi, Sasha Tsvyashchenko, Joshua Maynez, Abhishek Rao, Parker Barnes, Yi Tay, Noam Shazeer, Vinodkumar Prabhakaran, Emily Reif, Nan Du, Ben Hutchinson, Reiner Pope, James Bradbury, Jacob Austin, Michael Isard, Guy Gur-Ari, Pengcheng Yin, Toju Duke, Anselm Levskaya, Sanjay Ghemawat, Sunipa Dev, Henryk Michalewski, Xavier Garcia, Vedant Misra, Kevin Robinson, Liam Fedus, Denny Zhou, Daphne Ippolito, David Luan, Hyeontaek Lim, Barret Zoph, Alexander Spiridonov, Ryan Sepassi, David Dohan, Shivani Agrawal, Mark Omernick, Andrew M. Dai, Thanumalayan Sankaranarayana Pillai, Marie Pellat, Aitor Lewkowycz, Erica Moreira, Rewon Child, Oleksandr Polozov, Katherine Lee, Zongwei Zhou, Xuezhi Wang, Brennan Saeta, Mark Diaz, Orhan Firat, Michele Catasta, Jason Wei, Kathy Meier-Hellstern, Douglas Eck, Jeff Dean, Slav Petrov, Noah Fiedel. PaLM: Scaling Language Modeling with Pathways. arXiv preprint, 2022. ↩
-
Thomas Wang, Adam Roberts, Daniel Hesslow, Teven Le Scao, Hyung Won Chung, Iz Beltagy, Julien Launay, Colin Raffel. What Language Model Architecture and Pretraining Objective Work Best for Zero-Shot Generalization? arXiv preprint, 2022. ↩