Reinforcement Learning (RL) algorithms have recently demonstrated impressive results in challenging problem domains such as robotic manipulation, Go, and Atari games. But, RL algorithms typically require a large number of interactions with the environment to train policies that solve new tasks, since they begin with no knowledge whatsoever about the task and rely on random exploration of their possible actions in order to learn. This is particularly problematic for physical domains such as robotics, where gathering experience from interactions is slow and expensive. At the same time, people often have some intution about the right kinds of things to do during RL tasks, such as approaching an object when attempting to grasp it – might it be possible for us to somehow communicate these intuitions to the RL agent to speed up its training?
Well, if we have some intuition about some of the things the agent ought to do, why not just hand-code or otherwise implement policies that do those things and throw them into the mix during training to help the agent explore well? Though we can’t just have the agent imitate these policies, since they may be suboptimal and only useful at certain (and not all) portions of the task, we can perhaps still use them to help the agent learn from them where it can and ultimately surpass them.
In other words, we argue that in domains like robotics one powerful way to speed up learning is to encode knowledge into an ensemble of heuristic solutions (controllers, planners, previously trained policies, etc.) that address parts of the task. Leveraged properly, these heuristics act as teachers guiding agent exploration, leading to faster convergence during training and better asymptotic performance. Given a state, each teacher would simply provide the action it would take in that state, and the RL agent can consider these action proposals in addition to what its own still-training policy suggests it should do.
For example, if the task is to search for items in a messy heap, we may be able to provide policies for grasping, placing, and pushing objects based on prior work. Since these are in themselves not solved problems these policies may not accomplish these tasks in the optimal way, but would still do them far better than an agent starting to learn from scratch, which probably would do nothing useful. We could then supply these teachers to the agent and have it benefit from them while learning:

But, learning with teachers also presents additional challenges – the agent now needs to learn which teachers (if any) to follow in any given state, and to avoid alternating between teachers that are offering contradictory advice.
To address these challenges we developed Actor-Critic with Teacher Ensembles (AC-Teach), a policy learning framework to leverage advice from multiple teachers where individual teachers might only offer useful advice in certain states, or offer advice that contradicts other teacher suggestions, and where the agent might need to learn behaviors from scratch in states where no teacher offers useful advice. In this post we shall explain how AC-Teach works, and demonstrate that it is able to leverage varying teacher ensembles to solve multi-step tasks while significantly improving sample complexity over baselines. Lastly, we will show that AC-Teach is not only able to generate policies using low-quality teacher sets but also surpasses baselines when using higher quality teachers, hence providing a unified algorithmic solution to a broad range of teacher attributes.
Why might leveraging teacher ensembles be tricky?
An intuitive first idea for leveraging teachers may be to execute actions from them some random proportion of the time, a technique known as Probabilistic Policy Reuse1. Before jumping to explaining AC-Teach, let’s establish why such an approach may not work well in our setting with two example robotics tasks – pick and place, and sweeping of a cube towards a goal location using a hook.
Behavioral policies can be sensitive to contradictory teachers
When an agent has no notion of commitment, the experience it collects withe the aid of teachers can be low quality due to teachers that offer contradictory advice:


Behavioral policies can be sensitive to partial teachers
When an agent overcommits to its choice of policy, the experience it collects can be low quality due to teachers that only address parts of the task:


AC-Teach manages a good balance of exploration and commitment
Qualitatively, we can now look at what AC-Teach does during training to get a sense for why it may work better than the above approaches:


Problem Formulation
So, we can see above that several properties of teachers make them more tricky to utilize. Specifically, we make minimal assumptions on the quality of such teacher sets and assume that the sets can have the following attributes:
- partial: Individual teachers might only offer useful advice in certain states
- contradictory: Teachers might offer advice that contradicts other teacher suggestions
- insufficient: There might be states where no teacher offers useful advice, and the agent needs to learn optimal behavior from scratch
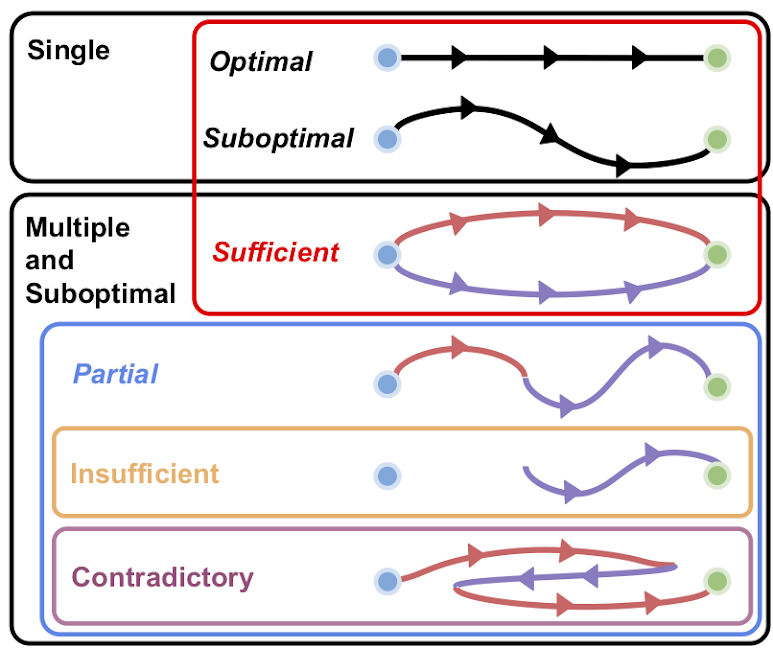
While prior work has addressed the problem of policy learning with teachers, we are the first to enumerate the above teacher attributes and propose a unifying algorithmic framework that efficiently exploits the set of teachers during the agent’s training regardless of the teachers’ attributes.
More concretely, we consider the policy advice setting in which the behavioral policy \(\pi_b\) (that is, the policy with which we collect experience during trainig, which is distinct from the agent policy \(\pi_\theta\)) can receive action suggestions from a set of teacher policies \(\Pi = \{\pi_1, \pi_2, \ldots, \pi_N\}\) that are available during training but not at test time. The problem is then to specify a behavioral policy \(\pi_b\) that efficiently leverages the advice of a set \(\Pi\) of teacher policies to generate experience to train an agent policy \(\pi_\theta\) with the goal of achieving good test-time performance in minimal train-time environment interactions.
Background Review
There are multiple methods to maximize the RL objective based on the policy gradient theorem, and one family of solutions is actor-critic methods. These methods train two networks – (1) the critic, which takes in an action and state and is optimized to output the expected return from taking that action and then acting via the optimal policy, and (2) the actor, which which takes in a state and is optimized to output the best action according to the critic.
Although AC-Teach is compatible with any actor-critic algorithm, in this work we focus on an instance of it implemented with Bayesian DDPG23, a popular actor-critic algorithm for continuous action spaces. The agent policy \(\pi_{\theta}\) in AC-Teach is the actor in the DDPG architecture. DDPG maintains a critic network \(Q_{\phi}(s, a)\) and a deterministic actor network \(\pi_{\theta}(s)\) (the agent policy), parametrized by \(\phi\) and \(\theta\) respectively. A behavioral policy \(\pi_b\) (usually the same as the agent policy, \(\pi_{\theta}\), with an additional exploration noise) is used to select actions that are executed in the environment, and state transitions are stored in a replay buffer \(\mathcal{B}\). DDPG alternates between collecting experience and sampling the buffer to train the policy \(\pi_{\theta}\) and the critic \(Q_{\phi}\).
The critic is trained via the Bellman residual loss and the actor is trained with a deterministic policy gradient update to choose actions that maximize the critic with a target critic and actor networks. The stability and performance of DDPG varies strongly between tasks. To alleviate these problems, Henderson et al. introduced Bayesian DDPG, a Bayesian Policy Gradient method that extends DDPG by estimating a posterior value function for the critic. The posterior is obtained based on Bayesian dropout4 with an \(\alpha\)-divergence loss. AC-Teach trains a Bayesian critic and actor in a similar fashion.
AC-Teach
In this section we explain the details of how AC-Teach works. AC-Teach is shaped by four key challenges with regards to how to implement an efficient behavioral policy:
-
How to evaluate the quality of the advice from any given teacher in each state for a continuous state and action space? AC-Teach is based on a novel critic-guided behavioral policy that evaluates both the advice from the teachers as well as the actions of the learner.
-
How to balance exploitation and exploration in the behavioral policy? AC-Teach uses Thompson sampling on the posterior over expected action returns provided by a Bayesian critic to help the behavioral policy to select which advice to follow.
-
How to deal with contradictory teachers? AC-Teach implements a temporal commitment method based on the posterior from the Bayesian critic that executes actions from the same policy until the confidence in return improvement from switching to another policy is significant.
-
How to alleviate extrapolation errors in the agent arising from large differences between the behavioral and the agent policy, the ‘‘large off-policy-ness’’ problem? AC-Teach introduces a behavioral target into DDPG’s policy gradient update, such that the critic is optimized with the target Q-value of the behavioral policy rather than the agent policy.
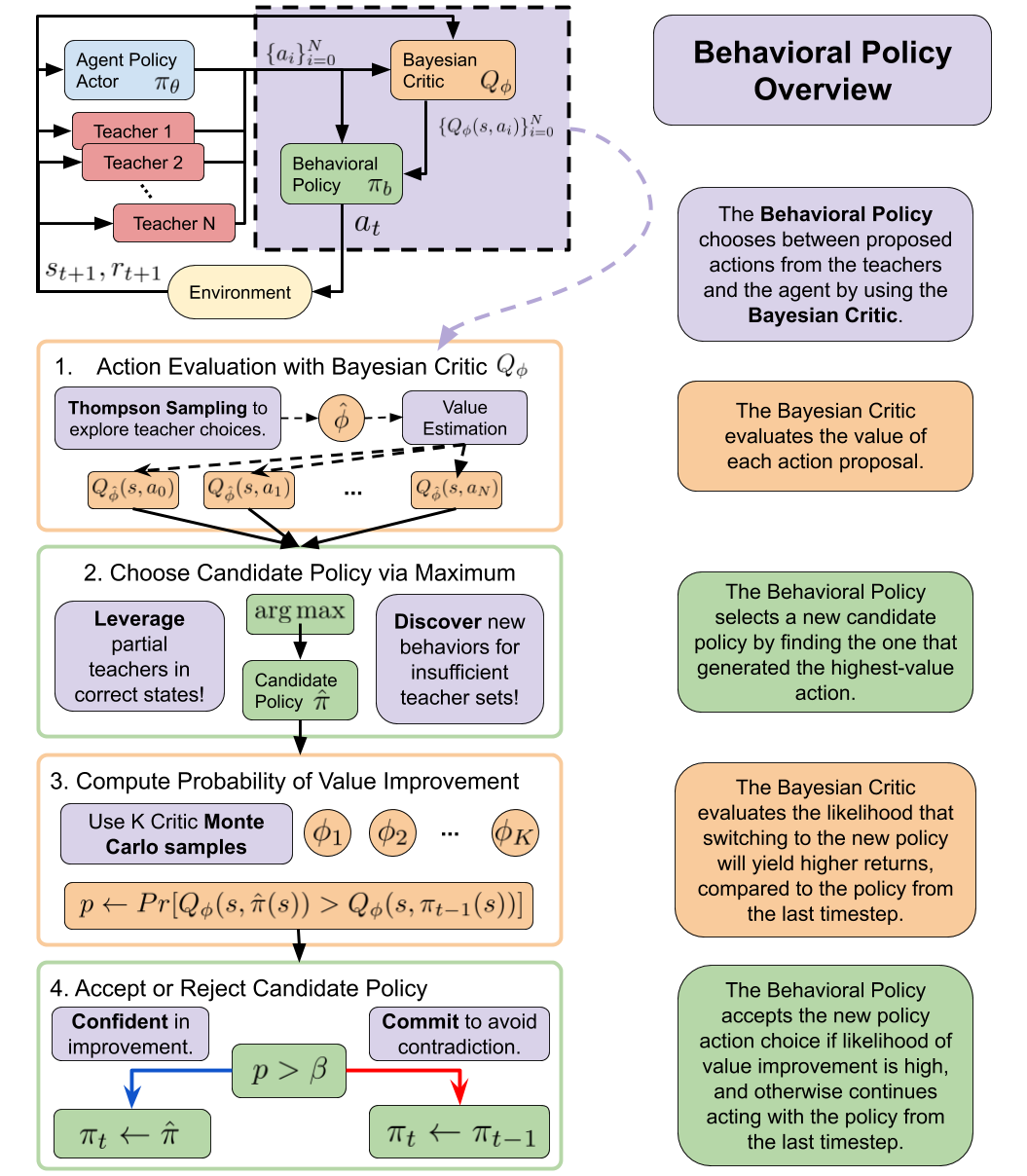
Critic-Guided Behavioral Policy
In off-policy Deep RL, the behavioral policy \(\pi_{b}\) collects experience in the environment during training and is typically the output of the actor network \(\pi_{\theta}\) with added noise. However, when teachers are available, the behavioral policy should take their advice into consideration. To leverage teacher advice for exploration, we propose to use the critic to implement \(\pi_b\) in AC-Teach as follows:
- Given a state S, the agent policy \(\pi_{\theta}\) and each teacher policy \(\pi_i \in \Pi\) generate a set of action proposals \({\pi_{\theta}(s),\pi_1(s),\ldots,\pi_N(s)}\).
- The critic \(Q_{\phi}\) evaluates the set of action proposals and selects the most promising one to execute in the environment.
This is equivalent to selecting between the teachers and the agent, but notice that this selection mechanism is agnostic to the source of the actions, enabling AC-Teach to scale to large teacher sets.
Thompson Sampling over a Bayesian Critic for Behavioral Policy
The behavioral policy needs to balance between exploration of teachers, whose utility in different states is not known at the start of training, and the agent policy, whose utility is non-stationary during learning versus exploitation of teachers that provided highly rewarded advice in the past. Inspired by the similarity between policy selection and the multi-arm bandits problem, we use Thompson sampling, a well-known approach for efficiently balancing exploration and exploitation in the bandit setting. Thompson sampling is a Bayesian approach for decision making where the uncertainty of each decision is modeled by a posterior reward distribution for each arm. In our multi-step setting, we model the posterior distribution over action-values using a Bayesian dropout critic network similar to Henderson et al.
Concretely, instead of maintaining a point estimate of \(\phi\) and \(Q_{\phi}\), we maintain a distribution over weights, and consequently over values by using Bayesian dropout. To evaluate an action for a given state-action pair, a new dropout mask is sampled at each layer of \(Q_{\phi}\), resulting in a set of weights \(\hat{\phi}\), and then a forward pass through the network results in a sample \(Q_{\hat{\phi}}(s, a)\). We then use critic \(Q_{\hat{\phi}}\) to evaluate the set of action proposals \({a_0,a_1,\ldots,a_N}\) and selects \(a_i = \arg\max_{a_0, a_1, ..., a_N} Q_{\hat{\phi}}(s, a)\) as the action to consider executing. The choice whether to execute this action depends on our commitment mechanism, explained next.
Confidence Based Commitment
In our problem setup, we consider the possibility of contradictory advice from different teachers that hinders task progress. Therefore, it is crucial to avoid switching excessively between teachers and commit to the advice from the same teacher for longer time periods. This is particularly important at the beginning of the training process when the critic has not yet learned to provide correct evaluations.
To achieve a longer time commitment, we compare the policy selected at this timestep \(\pi_i\) via the Thompson Sampling process to the policy selected at the previous timestep, \(\pi_j\). We use the posterior critic to estimate the probability for the value of \(a_i\) to be larger than the value of \(a_j\). If the probability of value improvement is larger than a threshold \(\beta\psi\^{t_c}\), the behavioral policy acts using the new policy, otherwise it acts with the previous policy. The threshold \(\beta\) controls the behavioral policy’s aversion to switch, and \(\psi\) controls the degree of multiplicative decay, to prevent over-commitment and make it easier to switch the policy choice when a policy is selected for several consecutive time steps.
To summarize, the following figure provides an overview of how the AC-Teach behavioral policy works:
Or, expressed more formally:

Addressing Extrapolation Error in the Critic
Off-policy learning can be unstable for deep reinforcement learning approaches. We follow Henderson et al.3 for training the learner policy \(\pi_{\theta}\) and the Bayesian critic \(Q_{\phi}\) on samples from the experience replay \(\mathcal{B}\). However, we further improved the stability of training by modifying the critic target values used for the \(\alpha\)-divergence Bayesian critic loss. Instead of using \(r + \gamma Q_{\phi'}(s', \pi_{\theta'}(s'))\) as the target value for the critic, we opt to use \(r + \gamma Q_{\phi'}(s', \pi_{b}(s'))\).
In other words, the behavioral policy is used to select target values for the critic. We observed that using this modified target value in conjunction with basing the behavioral policy on the critic greatly improved off-policy learning.
Experiments
We designed AC-Teach to be able to leverage experience from challenging sets of teachers that do not always provide good advice (see Table 1). In our experiments, we compare AC-Teach to other learning algorithms that use experience from teachers with the aforementioned attributes (see Sec. 3) for the following three control tasks (see Appendix D.1 for more task details). We outline the tasks and teacher sets below. For each task, we design a sufficient teacher that can complete each task that chooses the appropriate partial teacher to query per state, and unless differently specified, we add a Gaussian action perturbation to every teacher’s actions during learning so that their behavior is more suboptimal.
Path Following

Objective: a point agent starts each episode at the origin of a 2D plane and needs to visit the four corners of a square centered at the origin. These corners must be visited in a specific order that is randomly sampled at each episode. The agent applies delta position actions to move.
Teacher Set: we designed one teacher per corner that, when queried, moves the agent a step of maximum length closer to that corner. Each of these teachers ispartialsince it can only solve part of the task (converging to the specific corner). The four teachers are needed for the teacher set to be sufficient.
Pick and Place

Objective: pick up a cube and place it at a target location on the table surface. The initial position of the object and the robot end effector are randomized at each episode start, but the goal is constant. The agent applies delta position commands to the end effector and can actuate the gripper.
Teacher Set: we designed two partial teachers for this task, pickandplace. The pick teacher moves directly toward the object and grasps it when close enough. The place agent is implemented to move the grasped cube in a parabolic motion towards the goal location and dropping it on the target location once it is overhead.

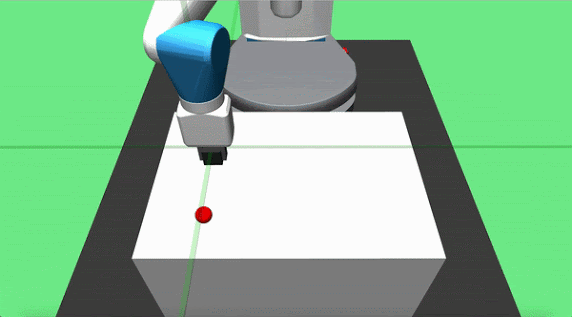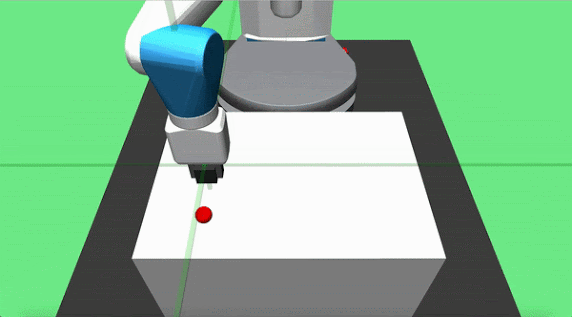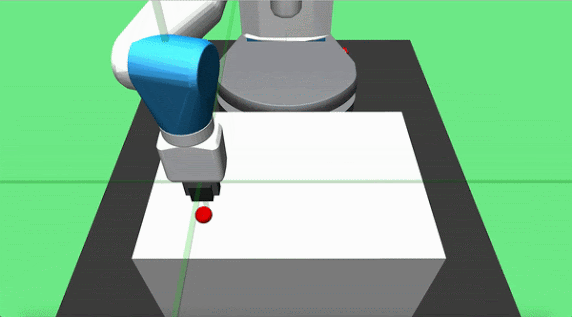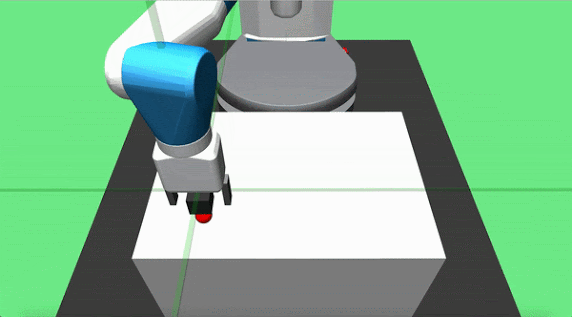
Hook Sweep

Objective: actuate a robot arm to move a cube to a particular goal location. The cube is initialized out of reach of the robot arm, and so the robot must use a hook to sweep the cube to the goal. The goal location and initial cube location are randomized such that in some episodes the robot arm must use the hook tosweep the cube closer to its base and in other episodes the robot arm must use the hook to push the cube away from its base to a location far from the robot.
Teacher Set: We designed four partial teachers for this task, hook-pick, hook-position, sweep-in, and sweep-out. The hook-pick teacher guides the end-effector to the base of the hook and grasps the hook. The hook-position teacher assumes that the hook has been grasped at the handle and attempts to move the end effector into a position where the hook would be in a good location to sweep the cube to the goal. Note that this teacher is agnostic to whether the hook has actually been grasped and tries to position the arm regardless. The sweep-in and sweep-out teachers move the end effector toward or away from the robot base respectively such that the hook would sweep the cube into the goal, if the robot were holding the hook and the hook had been positioned correctly, relative to the cube.



Baselines
We compare AC-Teach against the following set of baselines:
- BDDPG: Vanilla DDPG without teachers, using a Bayesian critic as in Henderson et al.
- DDPG + Teachers (Critic): Train a point estimate of the critic parameters instead of using Bayesian dropout. The behavioral policy still uses the critic to choose a policy to run.
- BDDPG + Teachers (Random): BDDPG with a behavioral policy that picks an agent to run uniformly at random.
- BDDPG + Teachers (DQN): BDDPG with a behavioral policy that is a Deep Q Network (DQN), trained alongside the agent to select the source policy as in Xie et al.
Results
We will highlight experiments that answer the following questions:
-
To what extent does AC-Teach improve the number of interactions needed by the agent to learn to solve the task by leveraging a set of teachers that are partial?
-
Can AC-Teach still improve sample efficiency when the set of teachers is insufficient and parts of the task must be learned from scratch?
-
Do all the components of AC-Teach help in it performing well?
Partial Sufficient Teacher Results
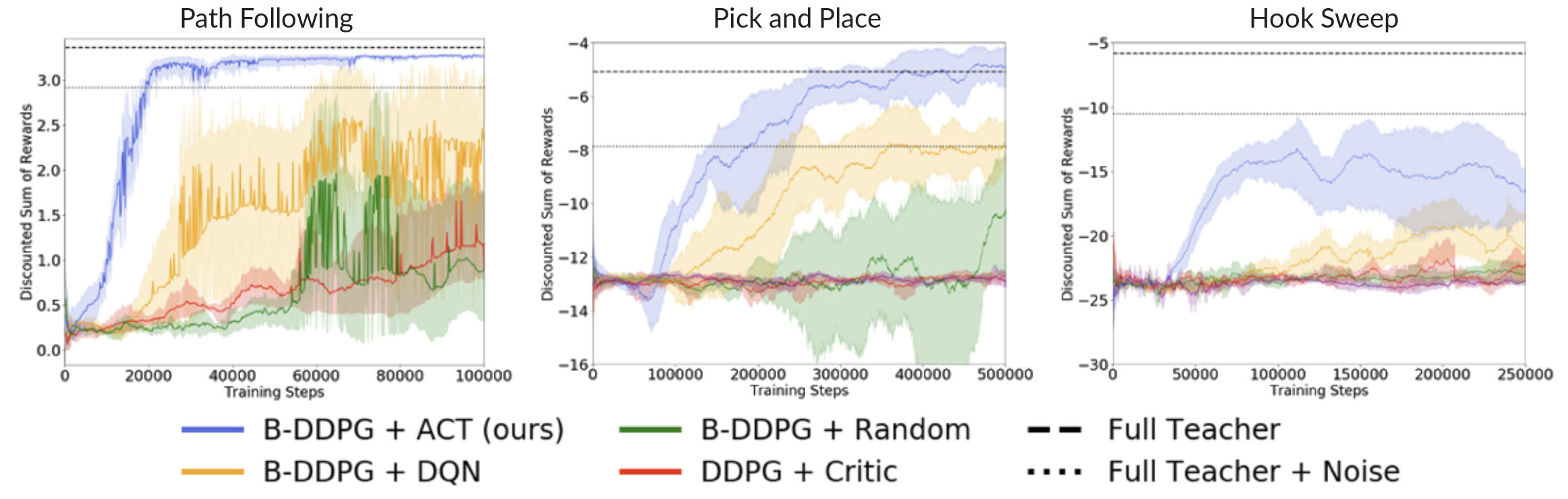
Above we present the test time performance of an agent trained with AC-Teach and baselines with the help of the sufficient partial teacher sets. For all the tasks, our method significantly outperforms all others in both convergence speed and asymptotic performance. On the pick-and-place task, the AC-Teach agent even outperforms our hand-coded teacher without noise, despite it being very close to optimal.
Partial Insufficient Teacher Results
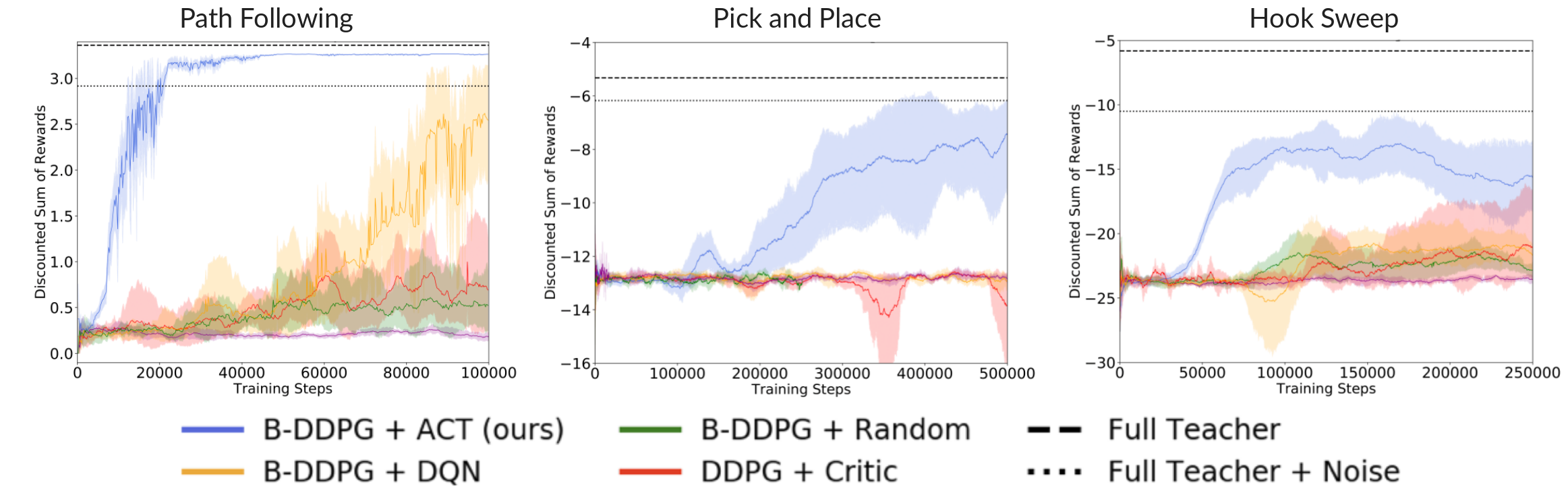
Above, we present the test time performance of agents trained with insufficient teacher sets, meaning we exclude one of the teachers from the ensemble for each task (for the pick-and-place task it is the place teacher, and otherwise we remove one teacher at random). AC-Teach can learn to accomplish the task even with insufficient teacher ensembles.
Ablation Results
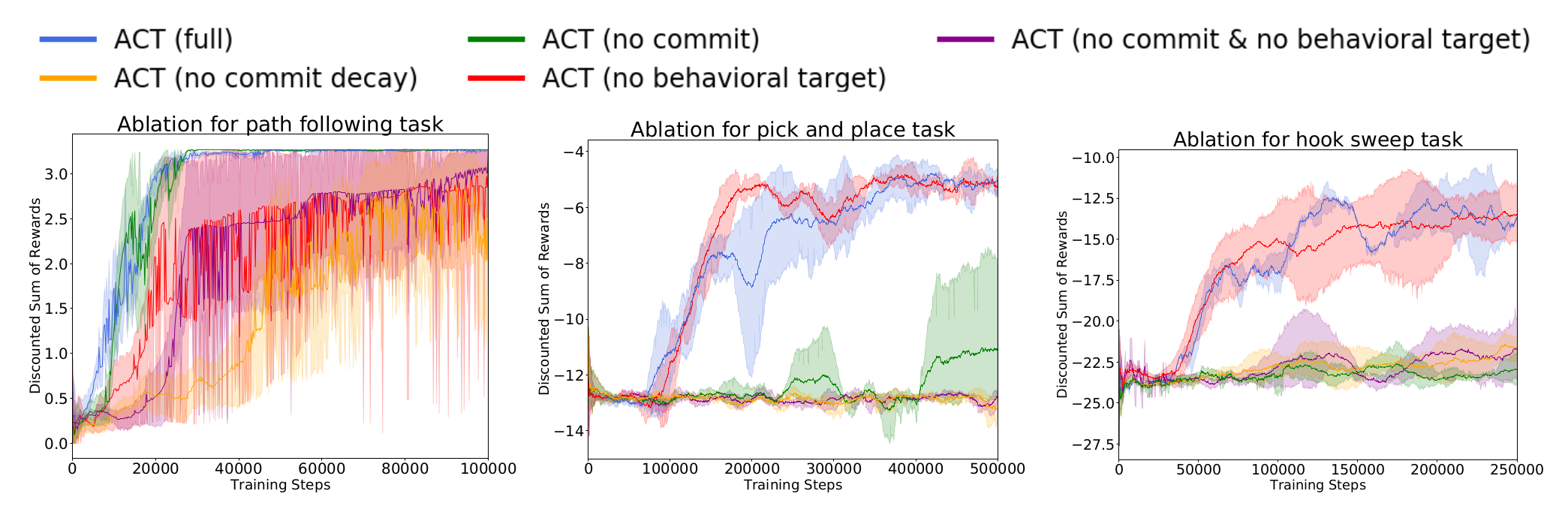
Above, we present the test time performance of agents trained with several modified versions of AC-Teach to evaluate the effect of each of its components, in particular different variants of time commitment and behavioral target. Interestingly, time commitment does not grant any benefit in the Path Following task despite being useful in the Pick and Place and Hook Sweep tasks. On the contrary, the behavioral target is not relevant for the performance of AC-Teach in the Pick and Place and Hook Sweep tasks despite being important in the Path Following.
We hypothesize that the tasks present different characteristics that benefit (or not) from the features of AC-Teach. In the case of Path Following, it includes little stochasticity and so the potential extrapolation error that is countered with the behavioral target is larger. For the Pick and Place task, both the end-effector and cube locations are randomized so the collected experience is varied enough, making extrapolation error less problematic. However, the shorter time horizon to complete the Pick and Place task and the possibility of pushing the cube away make commitment beneficial.
Learned Qualitative Agent Behaviors
Path Following: The agent mostly learns to follow optimal straight line paths to the waypoints, despite the teachers having noisy actions and exhibiting imperfect behavior at train time.

Pick and Place: Notice how the agent learned to grasp the cube and then slide it to the goal, even though the place teacher actually lifts the cube up and tries to execute a parabolic arc to the goal (see Place teacher above). The agent can learn to exhibit behavior that is different than that of the teachers in order to maximize task performance.

Hook Sweep: This agent learned to recognize situations where it needs to use the hook to sweep the cube forward to the goal, and where it needs to use the hook to pull the cube back to the goal.

Conclusion
We presented AC-Teach, a unifying approach to leverage advice from an ensemble of sub-optimal teachers in order to accelerate the learning process of an actor-critic agent. AC-Teach incorporates teachers’ advice into the behavioral policy based on a Thomson sampling mechanism on the probabilistic evaluations of a Bayesian critic. Our experiments and comparison to baselines showed that AC-Teach can extract useful exploratory experiences when the set of teachers is noisy, partial, incomplete, or even contradictory. In the future, we plan to apply AC-Teach to real robot policy learning to demonstrate its applicability to solving challenging long-horizon manipulation in the real world.
This blog post is based on the CoRL 2019 paper AC-Teach: A Bayesian Actor-Critic Method for Policy Learning with an Ensemble of Suboptimal Teachers by Andrey Kurenkov, Ajay Mandlekar, Roberto Martin-Martin, Silvio Savarese, Animesh Garg
For further details on this work, check out the paper on Arxiv.
-
Fernández, Fernando, and Manuela Veloso. “Probabilistic policy reuse in a reinforcement learning agent.” Proceedings of the fifth international joint conference on Autonomous agents and multiagent systems. ACM, 2006. ↩
-
Lillicrap, Timothy P., et al. “Continuous control with deep reinforcement learning.” arXiv preprint arXiv:1509.02971 (2015). ↩
-
Henderson, Peter, et al. “Bayesian policy gradients via alpha divergence dropout inference.” arXiv preprint arXiv:1712.02037 (2017). ↩ ↩2
-
Gal, Yarin, and Zoubin Ghahramani. “Dropout as a bayesian approximation: Representing model uncertainty in deep learning.” international :conference on machine learning. 2016. ↩