Thin Junction Tree Filters
for Simultaneous Localization and Mapping

Mark A. Paskin

Simultaneous Localization and Mapping (SLAM) is a fundamental problem in mobile robotics: while a robot navigates in an unknown environment, it must incrementally build a map of its surroundings and, at the same time, localize itself within that map. One popular solution is to treat SLAM as an estimation problem and apply the Kalman filter; this approach is elegant, but it does not scale well: the size of the belief state and the time complexity of the filter update both grow quadratically in the number of landmarks in the map. This paper presents a filtering technique that maintains a tractable approximation of the belief state as a thin junction tree. The junction tree grows under filter updates and is periodically ``thinned'' via efficient maximum likelihood projections so inference remains tractable. When applied to the SLAM problem, these thin junction tree filters have a linear-space belief state and a linear-time filtering operation. Further approximation yields a filtering operation that is often constant-time. Experiments on a suite of SLAM problems validate the approach.

Papers

Conference paper available for download in pdf. (This paper won a Distinguished Paper Award at IJCAI 2003.)

@InProceedings{Paskin2003,
  AUTHOR        = {Mark A. Paskin},
  TITLE         = {Thin Junction Tree Filters for 
                   Simultaneous Localization and Mapping},
  BOOKTITLE     = {Proceedings of the Eighteenth International 
                   Joint Conference on Artificial Intelligence (IJCAI-03)},
  EDITOR        = {Georg Gottlob and Toby Walsh},
  PAGES         = {1157--1164},
  PUBLISHER     = {Morgan Kaufmann Publishers},
  ADDRESS       = {San Francisco, CA},
  YEAR          = {2003}
}

Technical report available for download in pdf.

@TechReport{Paskin2002,
  AUTHOR        = {Mark A. Paskin},
  TITLE         = {Thin Junction Tree Filters 
                   for Simultaneous Localization and Mapping},
  INSTITUTION   = {University of California, Berkeley},
  YEAR          = {2002},
  MONTH         = {September},
  TYPE          = {Computer Science Division Technical Report},
  NUMBER        = {CSD-02-1198}
}

Movies

• A simulated SLAM problem. This movie demonstrates a very noisy SLAM problem. The robot moves through a planar environment where point landmarks are spaced on a grid. The robot can rotate its heading and translate in the direction of its heading. The robot's controls (rotational and translational velocity) are subject to additive Gaussian noise, as are its odometry readings (of rotational and translational velocity). The robot receives range-bearing measurements of landmarks that are within a foward "visual cone"; the range measurements are corrupted by multiplicative Gaussian noise and the bearing measurements are corrupted by additive Gaussian noise. The robot tries to move in a square pattern, but fails miserably because of control noise. The landmark measurements are plotted relative to the true path, which of course, the robot does not know. [3.2 MB mpeg ]
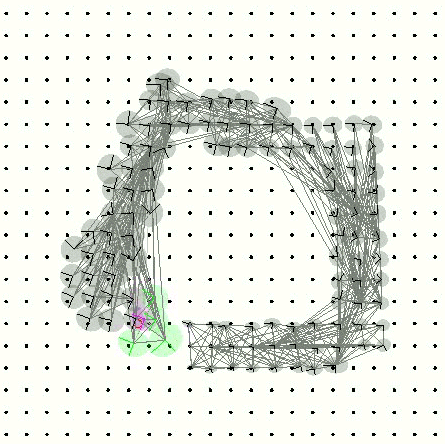
• The Kalman filter. This movie shows the belief state of the Kalman filter solution to the above problem. The marginal distributions of the robot and landmarks are shown by 95% confidence regions (landmarks in gray, robot in magenta, and currently-observed landmarks in green). The nonlinear motion and measurement models are linearized using the unscented transformation. This filter has knowledge of the true data association. [3.8 MB mpeg ]
• The Kalman filter with maximum likelihood data association. This setup is just as in the previous movie, except that the filter is not informed of the true data association; it uses maximum likelihood data association (Hungarian method) and gating. Landmark distributions are colored red if they are having a measurement incorrectly associated to them. [2.1 MB mpeg ]
• The FastSLAM filter (100 particles). This filter is given the true data association. The actual marginal distribution of each landmark is a mixture of Gaussians; this movie shows the maximum likelihood approximation of each mixture by a single Gaussian. [2.9 MB mpeg ]
• The FastSLAM filter (500 particles). This scenario is exactly as above, but the filter has five times as many particles. [3.3 MB mpeg ]
• The FastSLAM filter (100 particles) with more observations per time step. This problem has the same dynamics as the previous one, but the landmark grid is denser, leading to more observations per time step. [5.7 MB mpeg ]
• The Thin Junction Tree Filter (k = 16, h = 8, junction tree view). This movie shows the state of a thin junction tree filter whose clusters are constrained to contain no more than 16 variables (and whose separators may not contain more than eight variables). The junction tree is overlaid as follows: clusters are represented by squares; edges between clusters represent edges in the junction tree; edges between clusters and variables indicate membership in the cluster. [5.1 MB mpeg ]
• The Thin Junction Tree Filter (k = 10, h = 5, edge view). This movie shows the belief state of a thin junction tree filter whose clusters are constrained to contain no more than 10 variables (and whose separators may not contain more than five variables). The edges of the graphical model chosen by the filter are overlaid. [6.4 MB mpeg ]
• The Thin Junction Tree Filter (k = 16, h = 4, submap view). This movie shows the state of a thin junction tree filter whose clusters are constrained to contain no more than 16 variables (and whose separators may not contain more than four variables). For each cluster, the smallest bounding box for the cluster's landmarks is overlaid. [4.4 MB mpeg ]

Slides

• MURI Meeting (Stanford University, 7/17/2003) [pdf]
• IJCAI Conference (Acapulco, Mexico, 8/13/2003) [pdf]

Code

I am distributing the code I used to run my experiments (under the GNU public license), but be warned: this code is research-ware, pure and simple. While I was writing it, I made every attempt to document the code and to design it in a modular and extensible fashion. However, I have not had time to make the code fully presentable; for example, there is no manual. Thus, this code will probably be useful only to people that are willing to spend a decent amount of effort. I do think that the design of the library is easily understood from the documentation, and I think it could be very helpful to others that would like to code up SLAM algorithms—I spent a lot of time on object design.

The code comes in two parts:

1. A Java library. This library contains an implementation of the thin junction tree filter (specialized for SLAM), as well as the Kalman and Information filters. To see what's included, you can browse the documentation.
2. A Matlab interface to the Java library. This interface includes code to create SLAM simulations, run filters, and to visualize and analyze the results. To get a brief idea of what's included, you can check out the README.txt file.

This code is not supported, although I am happy to answer questions via e-mail. Furthermore, I do not plan to extend this code; I am currently working on a new implementation of the algorithms in Common Lisp, which has an object model that is far more flexible than that of Java.

Acknowledgements. This code uses (and includes) the JAMA Java matrix package. Some of the routines that count floating-point operations were adapted from routines in T. Minka's Lightspeed Matlab library. The Matlab library includes Niclas Borlin's implementation of the Hungarian algorithm, which is used for data association.