A key component of human-robot collaboration is the ability for robots to predict human behavior. Robots do this by building models of human decision making. One way to model humans is to pretend that they are also robots, and assume users will always choose the optimal action that leads to the best outcomes. It’s also possible to account for human limitations, and relax this assumption so that the human is noisily rational (their actions will usually lead to the ideal outcome, but are also somewhat random).
Both of these models work well when humans receive deterministic rewards: e.g., gaining either \(\$100\) or \(\$130\) with certainty. But in real-world scenarios, humans often need to make decisions under risk and uncertainty: i.e., gaining \(\$100\) all the time or \(\$130\) about \(80\)% of the time. In these uncertain settings, humans tend to make suboptimal choices and select the risk-averse option — even though it leads to worse expected outcomes! Our insight is that we should take risk into account when modeling humans in order to better understand and predict their behavior.

In this blog post, we describe our Risk-Aware model and compare it to the state-of-the-art Noisy Rational model. We also summarize the results from user studies that test how well Risk-Aware robots predict human behavior, and how Risk-Aware robots can leverage this model to improve safety and efficiency in human-robot collaboration. Please refer to our paper and the accompanying video for more details and footage of the experiments.
Motivation
When robots collaborate with humans, they must anticipate how the human will behave for seamless and safe interaction. Consider the scenario shown below, where an autonomous car is waiting at an intersection. The autonomous car (red) wants to make an unprotected left turn, but a human driven car (blue) is approaching in the oncoming lane.

The stoplight has just turned yellow for the human driven car. It is unclear whether the driver will accelerate — and try to make the light — or stop and play it safe. If the autonomous car thinks that the human will stop, it makes sense for the autonomous car to turn right; but if the robot anticipates that the human may try and make the light, it should wait for the human to go! Put another way, the robot needs to correctly anticipate what the human will do. And in order to do that, the robot needs to correctly model the human — i.e., correctly interpret how the human will make their decisions.
Background. Previous work has explored different approaches for robots tomodel humans. One common approach is to assume that humans also act like robots, and make perfectly rational decisions to maximize their utility or reward1. But we know that this isn’t always true: humans often make mistakes or suboptimal decisions, particularly when we don’t have much time to make a decision, or when the decision requires thinking about complex trade-offs. In recognition of this, today’s robots typically anticipate that humans will make noisily rational choices2. A noisily rational human is most likely to choose the best option, but there is also a nonzero chance that this human may act suboptimally, and select an action with lower expected reward. Put another way, this human is usually right, but occasionally they can make mistakes.
What’s Missing? Modeling people as noisily rational makes sense when humans are faced with deterministic decisions. Let’s go back to our driving example, where the autonomous car needs to predict whether or not the human will try to run the light. Here, a deterministic decision occurs when the light will definitely turn red in \(5\) seconds: the human knows if they will make the light, and can accelerate or decelerate accordingly. But in real world settings, we often do not know exactly what will happen as a consequence of our actions. Instead, we must deal with uncertainty by estimating risk! Returning to our example, imagine that if the human accelerates there is a \(95\)% chance of making the light and saving commute time, and a \(5\)% chance of running a red light and getting fined. It makes sense for the human to stop (since decelerating leads to the most reward in expectation), but a risk-seeking driver may still attempt to make the light.

Assuming that humans are rational or noisily rational doesn’t make sense in scenarios with risk and uncertainty. Here we need models that can incorporate the cognitive biases in human decision making, and recognize that it is likely that the human car will try and run the light, even though it is not optimal!
Insight and Contributions. When robots model humans as noisily rational, they miss out on how risk biases human decision-making. Instead, we assert:
To ensure safe and efficient interaction, robots must recognize that people behave suboptimally when risk is involved.
Inspired by work in behavioral economics, we propose using Cumulative Prospect Theory3 as a Risk-Aware model for human-robot interaction. As we’ll show, using the Risk-Aware model is practically useful because it improves safety and efficiency in human-robot collaboration tasks.
Modeling Humans: Noisy Rational vs Risk-Aware
Here we will formalize how we model human decision-making, and then compare the state-of-the-art Noisy Rational human model to our proposed Risk-Aware model.
Notation. We assume a setting where the human needs to select from a discrete set of actions \(\mathcal{A}_H\). Taking an action \(a_H \in \mathcal{A}_H\) may lead to several possible states, or outcomes. Returning to our driving example, the set of actions is \(\mathcal{A}_H = \{accelerating, stopping\}\), and choosing to accelerate may lead to making or running the light. Based on the outcome, the human receives some reward — ideally, the human will obtain as much reward as possible. For a given human action \(a_H\), we can express the expected reward across all possible outcomes as:
\[R_H(a_H) = p^{(1)}R^{(1)}_H(a_H) + p^{(2)}R^{(2)}_H(a_H), \cdots, p^{(K)}R^{(K)}_H(a_H)\]where \(p^{(k)}\) is the probability of outcome \(k\), and there are \(K\) possible outcomes. Overall, this equation tells us how valuable the choice \(a_H\) is to the human4.
The Rational Model. If the human behaved like a robot — and made perfectly rational decisions — then we might anticipate that the human will choose the action that leads to the highest reward \(R_H(a_H)\). Let’s use the Boltzmann distribution to write the probability of choosing action \(a_H\), and model the human as always choosing the action with the highest reward:
\[a_H^* = \text{arg}\max_{a_H} \frac{exp(R_H(a_H))}{\sum_{a \in \mathcal{A}_H}exp(R_H(a))}\]Our rational model is fairly straightforward: the human always chooses the most likely action. But we know this isn’t the case; humans often make mistakes, have cognitive biases, and select suboptimal options. In fact, Herbert Simon received a Nobel Prize and Turing Award for researching this very trend!
The Noisy Rational Model. We can relax our model so that the human usually chooses the best action:
\[P(a_H) = \frac{exp(\theta \cdot R_H(a_H))}{\sum_{a\in \mathcal{A}_H}exp(\theta \cdot R_H(a))}\]where \(\theta \in [0, \infty]\) is a temperature parameter, commonly referred to as the rationality coefficient. Tuning \(\theta\) tells us how frequently the human chooses the best action. When \(\theta \rightarrow \infty\), the human always picks the best action, and when \(\theta = 0\), the human chooses actions uniformly at random.
Uncertainty and Biases. One problem with the Noisy Rational model is that — no matter how we tune \(\theta\) — the model never thinks that a suboptimal action is most likely. This is problematic in real-world scenarios because humans exhibit cognitive biases that make it more likely for us to choose suboptimal options! Moving forward, we want to retain the general structure of the Noisy Rational model, while expanding this model to also recognize that there are situations where suboptimal actions are the most likely choices.
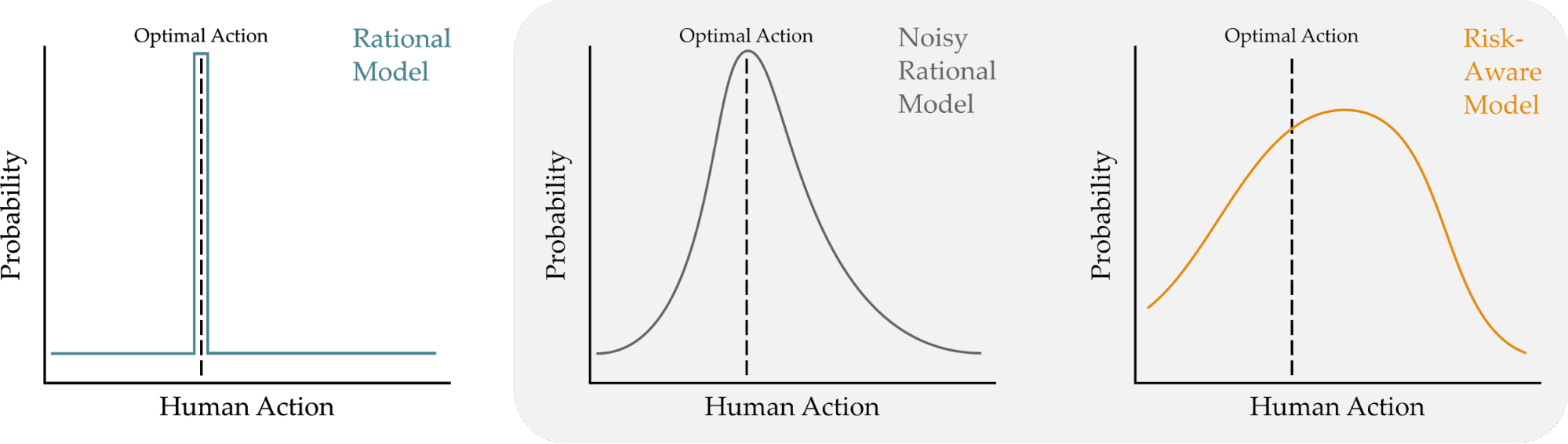
Our Risk-Aware Model. Drawing from behavioral economics, we adopt Cumulative Prospect Theory as a way to incorporate human biases under risk and uncertainty. This model captures both optimal and suboptimal decision-making by transforming the rewards and the probabilities associated with each outcome. We won’t go over all the details here, but we can summarize some of the major changes from the previous models.
-
Transformed rewards. There is often a difference between the true reward associated with a state and the reward the human perceives. For example, humans perceive the differences between large rewards (e.g., \(\$1\) million vs. \(\$1.01\) million) as smaller than the differences between low rewards (e.g., \(\$1\) vs. \(\$10,001\)). More formally, if the original reward of outcome \(k\) is \(R^{(k)}_H(a_H)\), we will write the human’s transformed reward as \(v\big(R^{(k)}_H(a_H)\big)\).
-
Transformed probabilities. Humans can also exaggerate the likelihood of outcomes when making decisions. Take playing the lottery: even if the probability of winning is almost zero, we buy tickets thinking we have a chance. We capture this in our Cumulative Prospect Theory model, so that if \(p^{(k)}\) is the true probability of outcome \(k\), then \(\pi_k\) is the transformed probability that the human perceives.
With these two transformations in mind, let’s rewrite the expected reward that the human associates with an action:
\[R_H^{CPT}(a_H) = \pi_1\cdot v\big(R^{(1)}_H(a_H)\big) + \pi_2\cdot v\big(R^{(2)}_H(a_H)\big), \cdots, \pi_K \cdot v\big(R^{(K)}_H(a_H)\big)\]What’s important here is that the expected reward that the human perceives is different than the real expected reward. This gap between perception and reality allows for the robot to anticipate that humans will choose suboptimal actions:
\[P(a_H) = \frac{exp(\theta \cdot R_H^{CPT}(a_H))}{\sum_{a \in \mathcal{A}_H}exp(\theta \cdot R_H^{CPT}(a))}\]Comparing our result to the Noisy Rational model, we use the same probability distribution to explain human actions, but now Risk-Aware robots transform both the rewards and probabilities to match known cognitive biases.
Summary. We have outlined two key ways in which we can model how humans make decisions in real-world scenarios. Under the Noisy Rational model, the optimal action is always the most likely human action. By contrast, our Risk-Aware model is able to predict both optimal and suboptimal behavior by non-linearly transforming rewards and probabilities.
Are Risk-Aware Robots Better at Predicting Human Actions?
Now that we’ve established how we are going to model humans, we want to determine whether these models are accurate. More specifically, we will compare our proposed Risk-Aware model to the current state-of-the-art Noisy Rational model. We will stick with our motivating scenario, where an autonomous car is trying to guess whether or not the human driven car will speed through a yellow light.
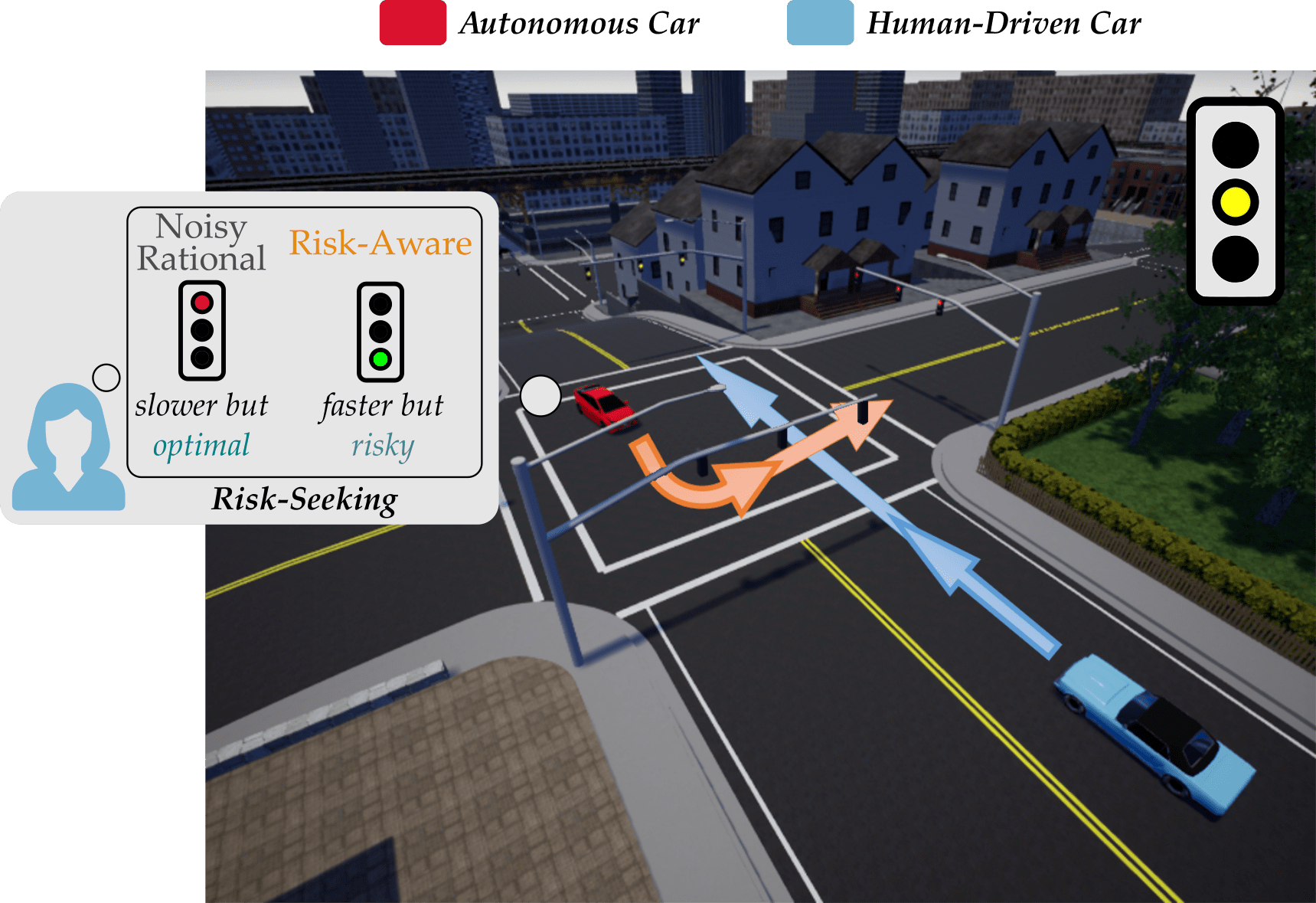
Autonomous Driving Task. Let’s say that you are the human driver (blue). Your car is a rental, and you are currently on your way to return it. If the light turns red — and you speed through — you will have to pay a \(\$500\) fine. But slowing down and stopping at the yellow light will prevent you from returning the rental car on time, which also has an associated late penalty. Would you accelerate (and potentially run the red light) or stop (and return the rental car with a late penalty)?
Experimental Overview. We recruited \(30\) human drivers, and asked them what action they would choose (accelerate or stop). To better understand what factors affected their decision, we varied the amount of information, time, and risk in the driving scenario:
- Information. We varied how much information the human drivers had about the likelihood of the light turning red. Participants were either given NO information (so that they had to rely on their personal prior), IMPLICIT information (where they got to observe the experiences of previous drivers), or EXPLICIT information (where they knew the exact probability).
- Time. We varied how quickly the human drivers had to make their decision. In TIMED, participants were forced to choose to stop or accelerate in under \(8\) seconds. In NOT TIMED, the participants could deliberate as long as necessary.
- Risk. Finally, we adjusted the type of uncertainty the human drivers faced when making their decision. In HIGH RISK the light turned red \(95\)% of the time, so that stopping was the optimal action. By contrast, in LOW RISK the light only turned red in \(5\)% of trials, so that accelerating became the optimal action.
Results. We measured how frequently the human drivers chose each action across each of these different scenarios. We then explored how well the Noisy Rational and Risk-Averse models captured these action distributions.
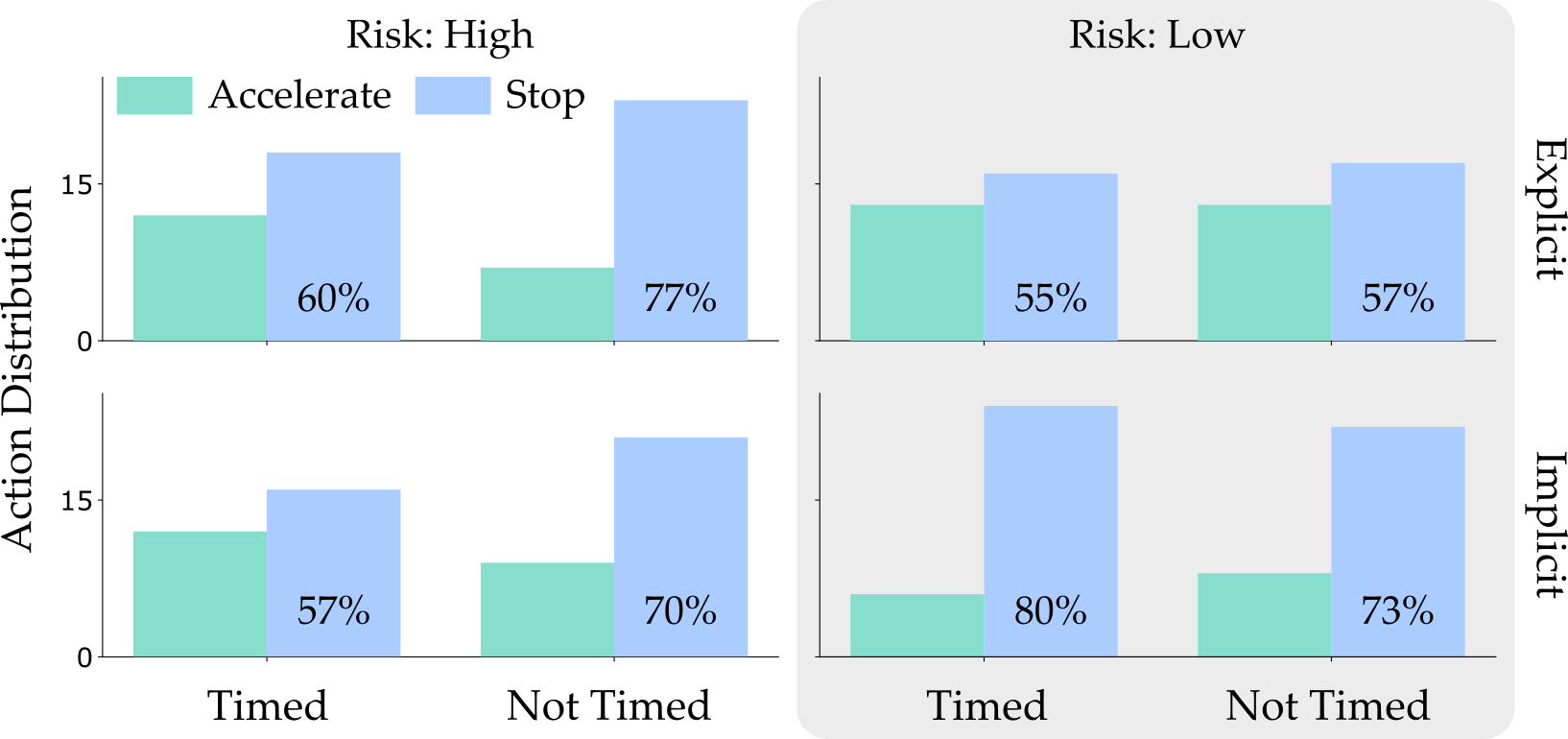
Action Distribution. Across all of our surveyed factors (information, time, and risk), our users preferred to stop at the light. We find that the most interesting comparison is between the High and Low Risk columns. Choosing to stop was the optimal option in the High Risk case (i.e. where the light turns red \(95\)% of the time) but stopping was actually the suboptimal decision in the Low Risk case when the light rarely turns red. Because humans behaved optimally in some scenarios and suboptimally in others, the autonomous car interacting with these human drivers must be able to anticipate both optimal and suboptimal behavior.
Modeling. Now that we know what the actual human drivers would do, how accurately can we predict these actions? We computed the Noisy Rational and Risk-Aware models that best fit our action distributions. To measure the accuracy of these models, we compared the divergence between the true action distribution and the models’ prediction (lower is better):
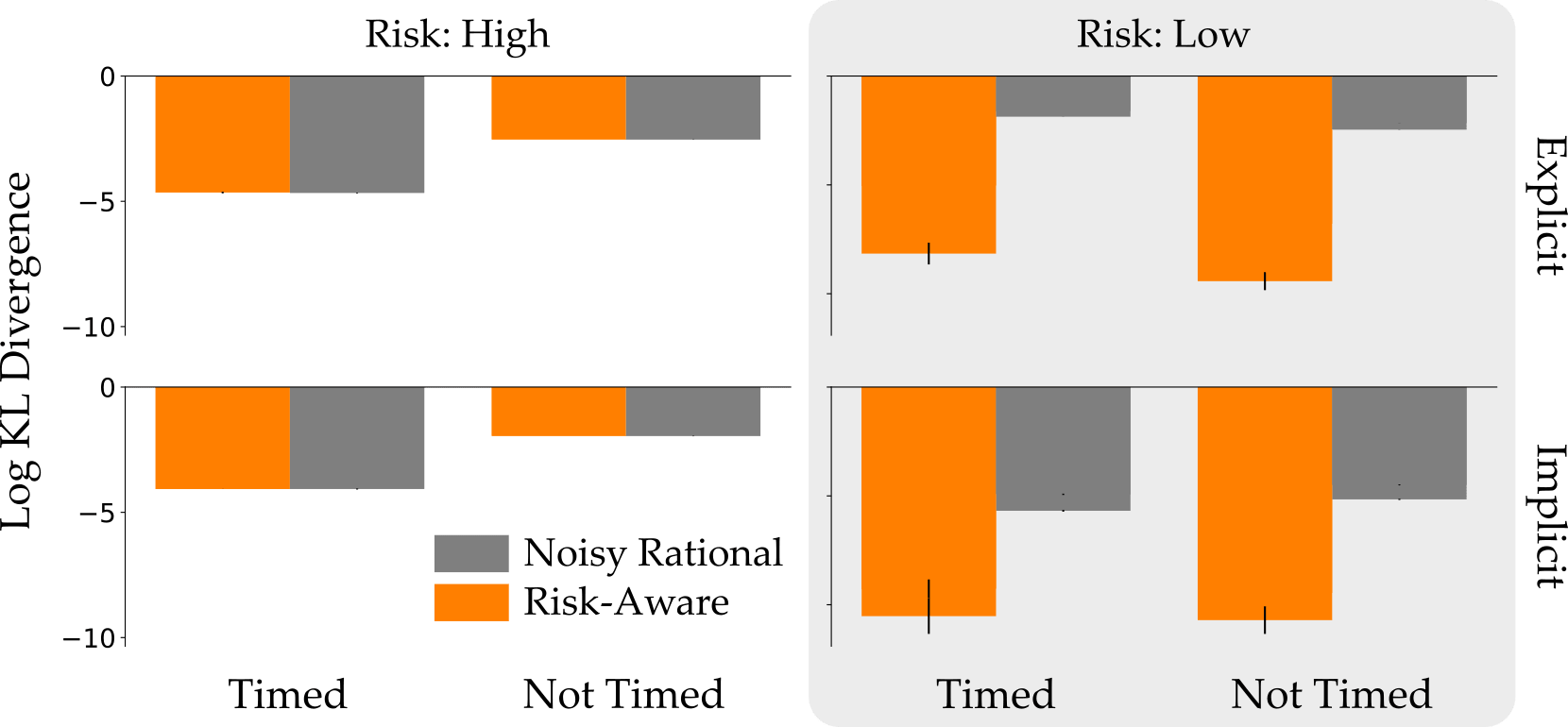
On the left you can see the High Risk case, where humans usually made optimal decisions. Here both models did an equally good job of modeling the human drivers. In the Low Risk case, however, only the Risk Aware model was able to capture the user’s tendency to make suboptimal but safe choices.
Why Risk-Aware is More Accurate. To understand why Risk Aware was able to get both of these scenarios right, let’s look at the human model. More specifically, let’s look at how the Risk-Aware model transformed the probabilities and rewards:
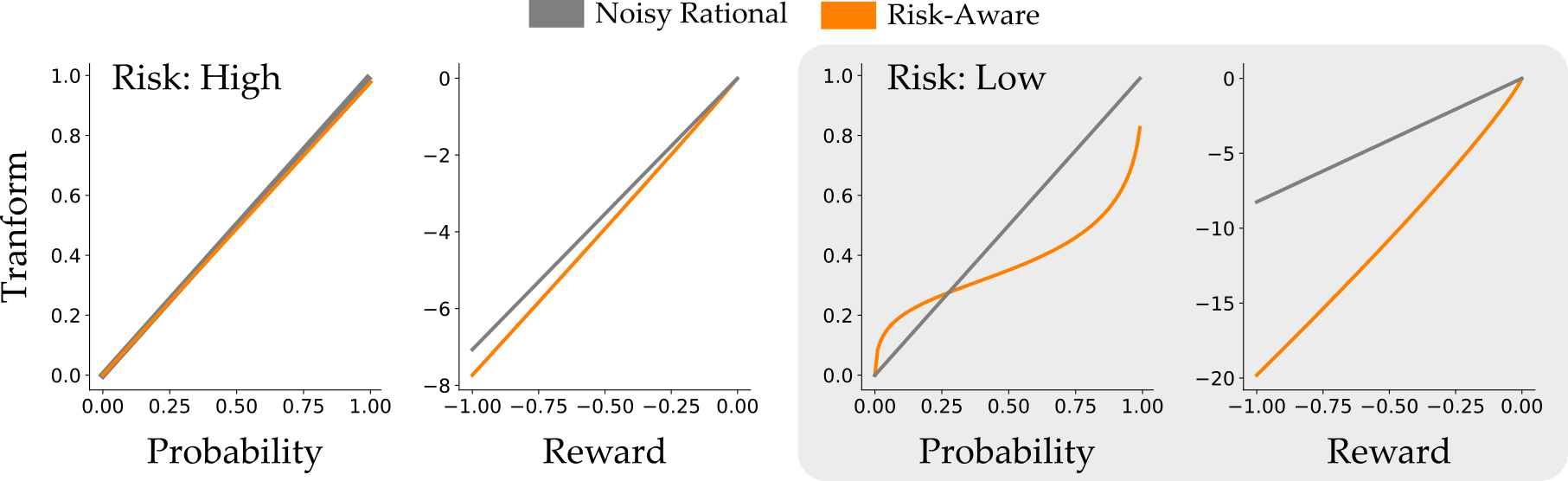
On the left we’re again looking at the High Risk scenario: the Risk-Aware model barely changes the probability and reward here. But when the light rarely turns red in Low Risk, the models diverge! The Risk-Aware model recognizes that human drivers overestimate both the probability that the light will turn red and the penalty for running the light. This enables the Risk-Aware model to explain why human drivers prefer to stop, even though accelerating is the optimal action.
Summary. When testing how human drivers make decisions under uncertainty, we found scenarios where the suboptimal decision was actually the most likely human action. While Noisy Rational models are unable to explain or anticipate these actions, our Risk-Aware model recognized that humans were playing it safe: overestimating the probability of a red light and underestimating the reward for making the light. Accounting for these biases enabled the Risk-Aware model to more accurately anticipate what the human driver would do.
Robots that Plan with Risk-Aware Models
We now know that Risk-Aware models can better predict suboptimal human behavior. But why is this useful? One application would be to leverage these models to improve safety and efficiency in human-robot teams. To test the usefulness of the Risk-Aware model, we performed a user study with a robotic arm, where participants collaborated with the robot to stack cups into a tower.
Collaborative Cup Stacking Task. The collaborative cup stacking task is shown below.

The human and robot are trying to stack all five cups to form a tower. There are two possible tower configurations: an efficient but unstable tower, which is more likely to fall, or an inefficient but stable tower, which requires more robot movement to assemble. Users were awarded \(20\) points for building the stable tower (which never fell) and \(105\) for building the unstable tower (which fell \(\approx 80\)% of the time). You can see examples of both types of towers below, with the efficient tower on the left and the stable tower on the right:


If the tower fell over, the human and robot team received no points! Looking at the expected reward, we see that building the efficient but unstable tower is actually the rational choice. But — building on our previous example — we recognize that actual users may prefer to play it safe, and go with the guaranteed success. Indeed, this tendency to avoid risk was demonstrated in our preliminary studies, where \(84\)% of the time users preferred to make the stable tower!
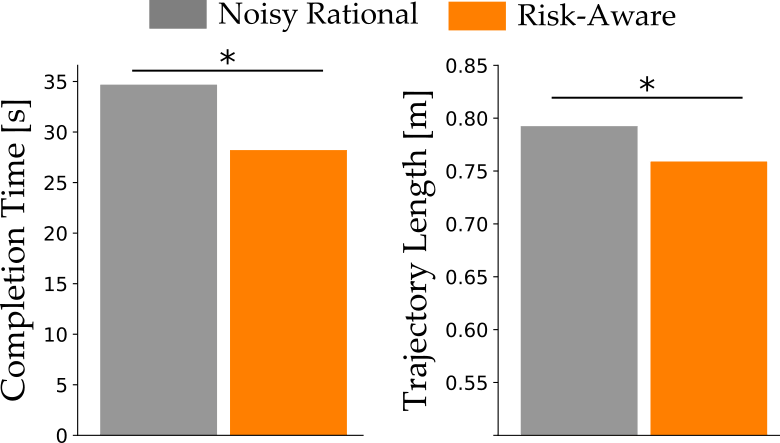
Experimental Overview. Each participant had \(10\) familiarization trials to practice building towers with the robot. During these trials, users learned about the probabilities of each type of tower collapsing from experience. In half of the familiarization trials, the robot modeled the human with the Noisy Rational model, and in the rest the robot used the Risk-Aware model. After the ten familiarization trials, users built the tower once with the Noisy Rational robot and the Risk-Aware robot. We measured efficiency (completion time) and safety (trajectory length) during collaboration. Because the robot had to replan longer trajectories when it interfered with the human, shorter trajectory lengths indicate safer interactions.
Model Predictions. The robot tried building the tower with two different models of the human: the Noisy Rational baseline and our Risk-Aware model. Planning with these models led the robot to choose two different trajectories:


Aggressive but Rational. When the robot is using the Noisy Rational model, it immediately goes for the closer cup, since this behavior is more efficient. Put another way, the robot using the Noisy Rational model incorrectly anticipates that the human wants to make the efficient but unstable tower. This erroneous prediction causes the human and robot to clash, and the robot has to undo its mistake (as you can see in the video above).


Conservative and Risk-Aware. A Risk-Aware robot gets this prediction right: it correctly anticipates that the human is overly concerned about the tower falling, and starts to build the less efficient but stable tower. Having the right prediction here prevents the human and robot from reaching for the same cup, so that they more seamlessly collaborate during the task!
Results. In our in-person user studies, participants chose to build the stable tower \(75\)% of the time. The suboptimal choice was more likely — which the Noisy Rational model failed to recognize. By contrast, our Risk-Aware robot was able to anticipate what the human would try to do, and could correctly guess which cup it should pick up. This improved prediction accuracy resulted in human-robot teams that completed the task more efficiently (in less time) and safely (following a shorter trajectory):
We also surveyed users to find their subjective response when working with these different robots. Our questions covered how enjoyable the interaction was (Enjoy), how well the robot understood human behavior (Understood), how accurately the robot predicted which cups they would stack (Predict), and how efficient users perceived the robot to be (Efficient). After they completed the task with both Noisy Rational and Risk-Aware robots, we also asked which type of robot they would rather work with (Prefer) and which robot better anticipated their behavior (Accurate):
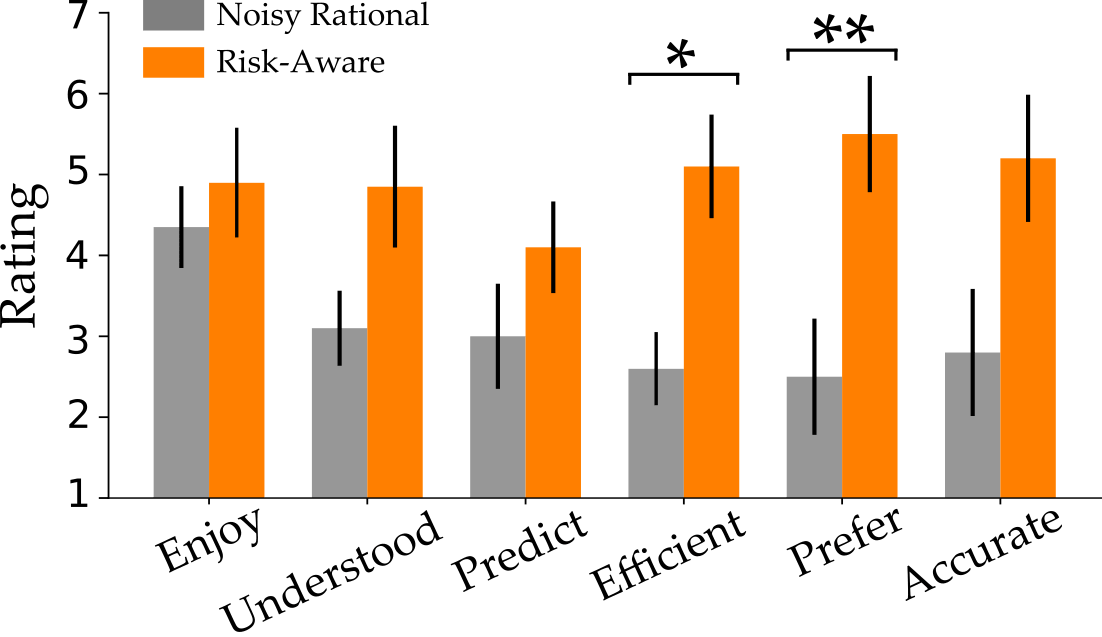
The participants’ responses to our survey are shown above. Each question was on a \(7\)-point Likert scale, where higher scores indicate agreement. We found that participants preferred the Risk-Aware robot, and thought it was more efficient than the alternative. The other scales favor Risk-Aware, but were not statistically significant.
Summary. Being able to correctly predict that humans will make suboptimal decisions is important for robot planning. We incorporated our Risk-Aware model into a robot working with a human during a collaborative task. This model led to improved safety and efficiency, and people also subjectively perceived the Risk-Aware robot as a better teammate.
Key Takeaways
We explored how we can better model human decision making under risk and uncertainty. Our main insight is that when humans are uncertain, robots should recognize that people behave suboptimally. We extended state-of-the-art prediction models to account for these suboptimal decisions:
- Existing Rational and Noisy Rational models anticipate that the best option is always most likely to be chosen.
- We adopted Cumulative Prospect Theory from behavioral economics, and showed how it can explain and predict suboptimal decisions.
- In both an autonomous driving task and a collaborative block stacking task we found that the Risk-Aware model more accurately predicted human actions.
- Incorporating risk into robot predictions of human actions improves safety and efficiency.
Overall, this work is a step towards robots that can seamlessly anticipate what humans will do and collaborate in interactive settings.
If you have any questions, please contact Minae Kwon at: mnkwon@stanford.edu
Our team of collaborators is shown below!

This blog post is based on the 2020 paper When Humans Aren’t Optimal: Robots that Collaborate with Risk-Aware Humans by Minae Kwon, Erdem Biyik, Aditi Talati, Karan Bhasin, Dylan P. Losey, and Dorsa Sadigh.
For further details on this work, check out the paper on Arxiv.
-
Pieter Abbeel and Andrew Ng, “Apprenticeship learning via inverse reinforcement learning,” ICML 2004. ↩
-
Brian Ziebart et al., “Maximum entropy inverse reinforcement learning,” AAAI 2008. ↩
-
Amos Tversky and Daniel Kahneman, “Advances in prospect theory: Cumulative representation of uncertainty,” Journal of Risk and Uncertainty 1992. ↩
-
In this blog post we will deal with single-decision tasks. The generalization to longer horizon, multi-step games is straightforward using value functions, and you can read more about it in our paper! ↩