

|
|
||
|
Research on robotic manipulation has mainly focused on manipulating rigid objects so far. However, many important application domains require manipulating deformable objects, especially deformable linear objects (DLOs), such as ropes, cables, and sutures. Such objects are far more challenging to handle, as they can exhibit a much greater diversity of behaviors. We have developed a new motion planner for manipulating DLOs and tying knots (self-knots and knots around simple static objects) using cooperating robot arms. The planner constructs a topologically-biased probabilistic roadmap in the DLO's configuration space. Unlike in traditional motion planning problems, the goal is a topological state of the world, rather than a geometric one. The implemented planner has been tested in simulation to achieve various knots like bowline, neck-tie, bow (shoe-lace), and stun-sail. Possible applications of our planner are robotized suturing in medical surgery and assembly of cable harnesses in automobile industries.
|

|
|
||||
|
PRM planners have been successfully used to plan complex robot motions in configuration spaces of various dimensionalities. But their efficiency decreases dramatically in spaces with narrow passages. Here, we investigate a new method - which we call small-step retraction - that helps PRM planners find paths through such passages. The method relies on the empirical observation that widening narrow passages by only a small amount greatly facilitates the task of sampling configurations into them. So, it consists of slightly "fattening" the robot's free space, constructing a roadmap in the fattened free space, and finally repairing portions of this roadmap by retracting them out of collision into the actual free space. The fattened free space is not explicitly computed. Instead, the geometric models of the workspace objects (robot links and/or obstacles) are "thinned" around their medial axis (leftmost figure). A robot configuration lies in fattened free space if the thinned objects do not collide at this configuration. Two repair strategies are proposed. The "optimist" strategy waits until a complete path has been found in fattened free space before repairing it. Instead, the "pessimist" strategy repairs the roadmap as it is being built. The former is usually very fast, but may fail in some pathological cases where the computed path crosses "false" passages. The latter is more reliable, but not as fast. A simple combination of the two strategies yields an integrated planner that is both fast and reliable. This planner was implemented as an extension of a pre-existing single-query PRM planner, SBL (see MPK toolkit). Comparative tests on various examples show that it is significantly faster (sometimes by several orders of magnitude) than SBL.
|

|
|
||||
|
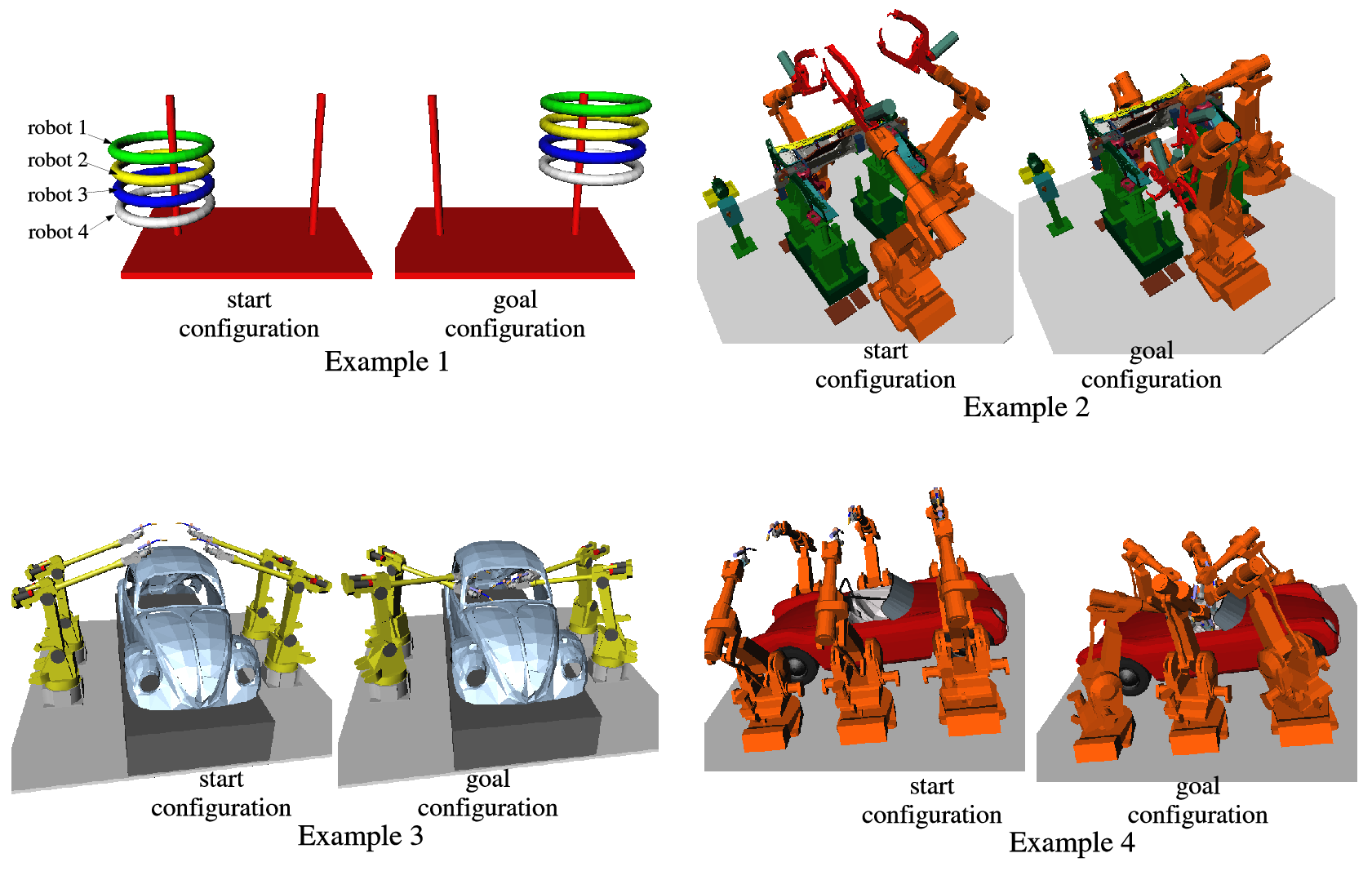
We consider a motion planning problem that occurs in tasks, such as spot welding, car painting, inspection, and measurement, where the end-effector of a robotic arm must reach successive goal placements given as inputs (the two leftmost figures show industrial examples of such scenarios). The problem is to compute a near-optimal path of the arm so that the end-effector visits each goal once. It combines two notoriously hard sub-problems - the collision-free shortest path and the traveling-salesman problems. It is further complicated by the fact that each goal placement of the end-effector may be achieved by several configurations of the arm - typically, distinct solutions of the arm's inverse kinematics (3rd figure from left). This leads us to construct a set of goal configurations of the robot that are partitioned into groups. The planner must compute a robot path that visits one configuration in each group and is near optimal over all configurations in every goal group and over all group orderings (rightmost figure). Our algorithm operates under the assumption that the computational cost of finding a good path between two goal configuration dominates that of finding a good tour in a graph of with edges of given costs. So, our algorithm tries to minimize the number of times it computes a path between two goal configurations. Although it still computes a quadratic number of such paths in the worst-case, experimental results show that it is much faster in practice. Our algorithm makes use of a recent approximation algorithm for the group Steiner tree problem [C. Chekuri, G. Even, and G. Kortsarz. A Greedy Approximation for the Group Steiner Problem. To appear in Discrete Applied Mathematics].
|

|
|

|

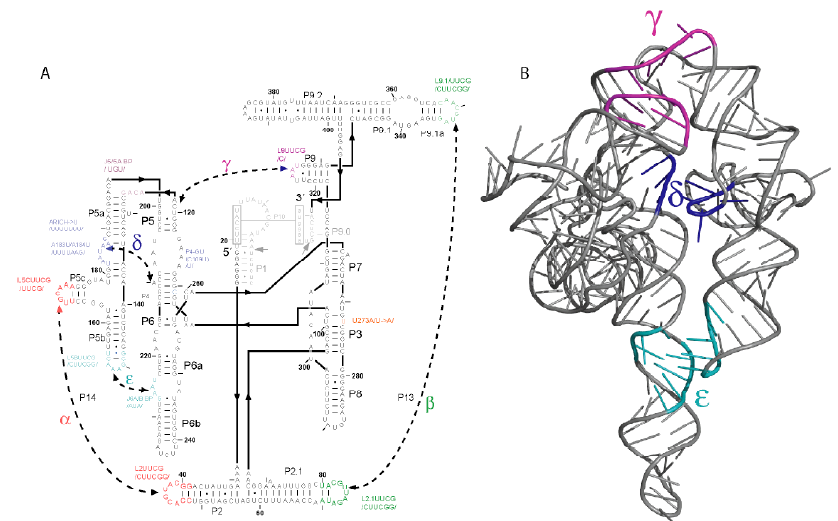
Webpages: |

|
 1(a) |
 1(b) |
 1(d) |
|
|

|

|
|
|